
¡Con naranjas se entiende!
Dicen los expertos en aprendizaje que el esfuerzo más grande que el cerebro humano hace en toda su vida es aprender a contar: ser capaz de relacionar un número (concepto abstracto) con una cantidad de algo y especialmente, que esa cantidad valga para cosas diferentes, tres caballos o tres flores.1
Todos los humanos conseguimos coronar ese puerto. El siguiente paso importante que debe hacer la cabecita de un chaval es la división, también relacionada con la abstracción y que vuelve a suponer otro reto para la mente.
“Divide y vencerás”
Conocer los conceptos no es sencillo pero conocerlos íntimamente, asumirlos, incluso intuirlos, es bastante más difícil.
Una división es la obtención de un valor relativo del numerador con relación a una unidad de denominador, en caso contrario, el numerador es un valor absoluto, sin referencia; o como indica el diccionario de la RAE:
“Averiguar cuántas veces una cantidad, llamada dividendo, contiene a otra, llamada divisor”.
Dicho así, de memoria, parece complejo pero, si se entiende, la operación es muy potente, tan potente que una definición del e-DRAE de división es:
“Modo de conocer las cosas, que sirve para dar clara idea de ellas”
Se puede abrir, con la división y la abstracción, una pequeña ventana al juego del pensamiento. Abstraer, tal y como lo define el diccionario de María Moliner, es separar mentalmente. Qué es dividir sino separar una cosa en partes iguales. Qué es entender si no hacer abstracción de un concepto para poder asimilarlo. Los animales no entienden porque no son capaces del inteligente ejercicio de la abstracción. Saber dividir es haber comprendido.
Es fácil saber dividir, pero no es fácil saber qué es una división. Y constato que no es fácil porque año tras año corroboro en la universidad que los alumnos no entienden que el módulo de deformación es la división entre la tensión de un elemento y su deformación unitaria, o sea
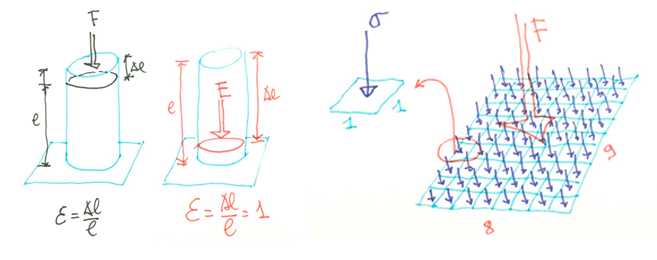
Dcha. Y una tensión (cociente entre fuerza y superficie) no es más que una fuerza relativa, o sea, la fuerza que actúa en una superficie unidad.
En cambio sí entienden, y lo sé porque se lo pregunto tal cual, que el precio de las naranjas es el cociente entre el precio total que pago por las naranjas y su peso en kilos. Basta trasladar ese entendimiento a la resistencia de materiales para entender el módulo.
Entienden también mucho mejor el comportamiento lineal si, en vez de explicarlo de forma matemática mediante una recta, les digo que “el frutero es lineal” si aplica siempre el mismo precio: si se llevan un kilo, un euro, si se llevan dos, dos euros. Y cada kilo de más que se lleven es un euro más.
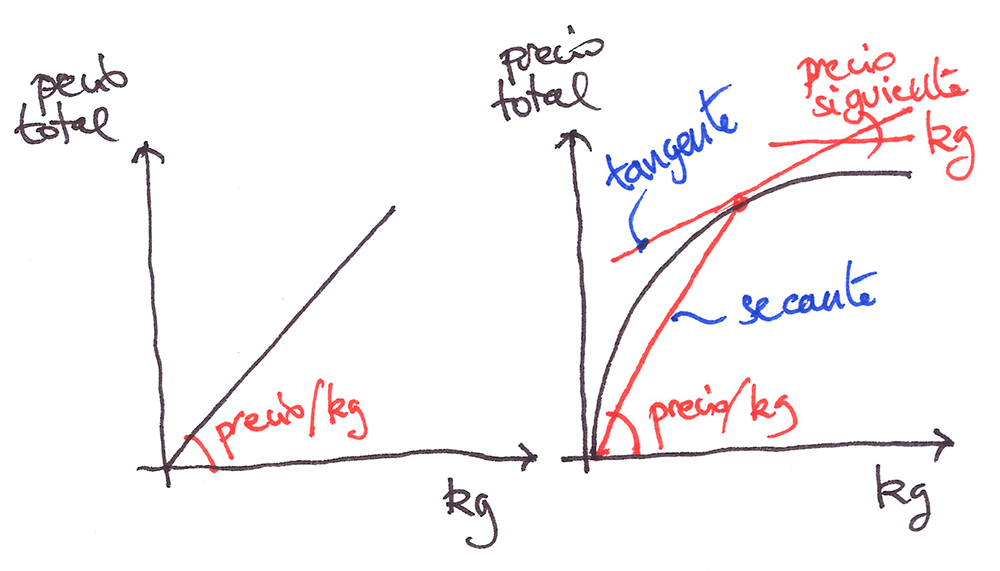
En cambio, el frutero se comportaría de forma no lineal cuando a mayor cantidad comprada menor precio unitario (pendiente de la recta secante). Esto tiene varias complicaciones operativas porque nunca sabes a priori cuanto va a costar el siguiente kilo (pendiente de la recta tangente) porque depende de los kilos totales comprados, sin embargo tiene una ventaja clarísima para comprador (paga menos) y para vendedor (vende más). En hormigón esta ventaja se llama ductilidad y supone ente otras ventajas que las vigas dúctiles antes de romperse se deforman mucho, ¡avisan!
También retiraría este esquema
“¡Con naranjas lo entienden!”
Si se les habla de dos magnitudes más abstractas, como las tensiones y las deformaciones, no entienden el cociente, no entienden la medida relativa que una división propone. Pero con naranjas, o con plátanos, lo entienden.

Y los profesores ¿lo entienden los profesores?
Feynman2, un famoso físico, científico, premio Nobel que dedicó una parte importante de su vida a reformular la teoría cuántica y otra parte de su vida científica a enseñar, cuenta que, en sus famosos (por juerguistas) viajes a Brasil le preguntaron en una Universidad por la razón de que no hubiese Premios Nobel de física brasileños y contestó que, por su conocimiento de las universidades, libros y profesores brasileños podía afirmar que éstos no sabían física y que su conocimiento se reducía a las retahílas leídas en los libros.
Esta imagen de enseñanza me recuerda, entre otras, a las clases de religión en las que se enseñaba mediante las letanías responsoriales de los catecismos.

Recuerdo una clase de matemáticas de 2º de carrera, con unas pizarras kilométricas escritas con un orden exquisito, impropias de una persona que sabe y explica, pero propias de una persona que copia. El profesor, de espaldas, estaba escribiendo y, a la vez, leyendo lo que escribía. En un momento determinado un alumno, que aún hoy no alcanzo a entender cómo podía estar siguiendo la clase, dijo:
“Perdone, no entiendo el paso que ha dado entre el final de la quinta línea y el principio de la sexta. El profesor giró su cara hacia el aulario, miró la quinta línea, miró sus apuntes, miró la sexta línea, frunció el ceño, cotejó y, con el gesto tranquilo, concluyó: perdonad ¡me he saltado una línea!”
El problema, como dice J.L.G. Quirós3 es que la ciencia es muy fácilmente imitable. Basta con conocer la farragosa jerga científica y matemática para poder embaucar con mayor o menor éxito. Esto pasa fácilmente en la relación profesor alumno, pero también pasa en la tecnología de alto nivel e, incluso en la alta ciencia. Casos de fraudes se han descubierto bastantes, habrá muchos otros danzando libres por los libros. Seguramente en este texto también. Su labor de lectores es no creérselo, criticar y reescribir.
¿Es posible otro tipo de enseñanza? Yo creo que sí
Una enseñanza en la que el profesor lo entienda, lo transmita con emoción y se preocupe de que el alumno lo reciba claro: Aprende a armar un muro en menos de 3 min.
¡Con naranjas se entiende!
Juan Carlos Arroyo (ingenio.xyz) ingeniero de camino.
Madrid, Noviembre 2016
Notas:
1 Los números primos; Enrique Gracián, Ed. RBA. Reseña: Enrique Gracián es un descubrimiento maravilloso si os gusta la divulgación científica.
2 ¿Está Ud. de broma Sr. Feynman? Aventuras de un curioso personaje; Richard P. Feynman. Ed. Alianza editorial. 1987, 6ª reimpr. 2003 Reseña: Aventuras de un premio nobel. Divertidísimo. No dejéis de leerlo.
3 Varios artículos de José Luis González Quirós. Reseña: Leer a José Luis G. Quirós es hacer un viaje de placer por la filosofía de la ciencia.







