Capítulo 5 del libro “Principios de la Estructura Urbana”, 2005, de Nikos A. Salíngaros
Traducción de María Fernanda Sánchez
Resumen. Los principios científicos aplicados a la forma de la ciudad ayudan a comprender el papel de los distintos tipos de conectividad urbana. El grado de “vida” de una ciudad o región de una ciudad está ligado a la complejidad de las conexiones visuales, geométricas y de los caminos. Existe una distribución óptima de las longitudes de las conexiones en una ciudad viva, y la violación de esta distribución elimina la vida del entorno urbano. Las parcelaciones alternativas de una ciudad viva revelan la compleja estructura necesaria para generar el contacto humano, que es la base de la vida en la ciudad. Estos resultados se comparan con el trabajo de Christopher Alexander.
1. Introducción
2. “Una ciudad no es un árbol” de Christopher Alexander
3. Parcelaciones alternativas de una ciudad viva
4. Módulos urbanos y fuerzas conectivas
5. Módulos urbanos y alineación geométrica
6. La homogeneización y la segregación destruyen la estructura del sistema
7. Dualidad entre los edificios y el espacio urbano
8. El control y la supresión del surgimiento
9. Las ciudades evolucionan su propia forma
10. La distribución de las longitudes conectivas
11. Los ecosistemas y la geometría
12. Conclusión
Introducción
¿Qué hay que hacer para arreglar la forma urbana inhumana? Cada vez es más evidente que no entendemos realmente cómo construir un entorno habitable. Estoy convencido de que la respuesta se encuentra fuera de los enfoques contemporáneos que derivan de los modos de pensamiento arquitectónico, en las técnicas desarrolladas para el análisis de sistemas complejos. Un gran sistema complejo contiene un enorme número de conexiones internas. Está formado por componentes de diversos tamaños, que se conectan e interactúan de manera particular para crear un todo coherente. La forma en que esto ocurre en diferentes casos se desprende de reglas muy generales derivadas de la biología y la informática. Hasta ahora, esos resultados han quedado fuera de la corriente principal del urbanismo.
Una importante excepción que va en sentido contrario es el trabajo de Christopher Alexander. A partir del clásico artículo “A City is Not a Tree” (Alexander, 1965), el posterior libro “A Pattern Language” (Alexander, Ishikawa et al., 1977) y su libro más reciente (Alexander, 2001), sus resultados sobre la forma arquitectónica y urbana se aplican ahora en informática y biología. El trabajo de Alexander contiene muchas soluciones a problemas de diseño urbano. Su artículo apareció originalmente en 1965 y fue aclamado como una declaración seminal sobre la estructura urbana; sin embargo, a pesar de haber sido reimpreso y traducido a varios idiomas, ha tenido poco impacto en el desarrollo de las ciudades desde entonces. Los arquitectos convencionales nunca adoptaron “A Pattern Language”, por lo que las ideas de Alexander y sus coautores parecen haber sido ignoradas por la profesión.
Ya es hora de que apreciemos el enfoque matemático de Alexander por las herramientas inmensamente poderosas que ofrece. Dichas herramientas permiten acceder a muchos resultados de disciplinas científicas distintas que podrían traducirse a términos relevantes para la estructura urbana. Además, la claridad del pensamiento científico protege la sensibilidad humana contra las fuerzas irracionales del diseño, que se dejan llevar por la moda y la búsqueda sin sentido de la novedad. Algunas de ellas se han incorporado al canon de diseño urbano actual, que se basa tanto en la ideología y la ignorancia como en las necesidades humanas. Las ciudades deberían estar configuradas de acuerdo con un conjunto de principios de diseño bien probados. Me gustaría derivar esas reglas.
El debate girará en torno a los nodos y sus interconexiones; cómo los nodos se conectan para formar módulos; y cómo los módulos se conectan para formar una ciudad. Las conexiones pueden adoptar diversas formas: acoplamiento geométrico de estructuras contiguas (Salingaros, 2000a), acoplamiento visual entre una persona y la información de una estructura (Mikiten, Salingaros et al., 2000; Salingaros, 1999), interacción entre seres humanos, acoplamiento peatonal de dos nodos geométricos o funcionales a través de un sendero (Salingaros, 1998), acoplamiento de transporte por carretera o metro entre nodos muy separados (Salingaros, 1998), etc.
Aunque se trata de nociones distintas de conectividad, resulta que todas están relacionadas. Los bordes geométricos, por ejemplo, proporcionan tanto una separación transversal como un posible conducto para las conexiones a lo largo del borde. Las interfaces urbanas actúan como separadores transversales para un tipo de flujo (por ejemplo, el de los automóviles) al tiempo que fomentan el tráfico peatonal a través de la interfaz. Por lo tanto, a efectos de este debate, me referiré simplemente a las conexiones como un concepto general e inclusivo, y no especificaré exactamente qué tipo de conexión está implicada.
“Una ciudad no es un árbol”, de Christopher Alexander
El título del primer artículo de Alexander es pegadizo, aunque un poco engañoso. Sí, una ciudad viva no sigue una estructura arbórea matemática, pero el argumento de Alexander es que la mayoría de las ciudades contemporáneas son árboles (Alexander, 1965). Los profesores han tenido en mente el modelo “arbóreo” al enseñar la forma de la ciudad, perpetuando así los principios urbanísticos de la posguerra que se basan en los árboles. Ahora construimos ciudades “arbóreas” y convertimos incuestionablemente las antiguas ciudades vivas en “árboles”; sin embargo, siempre que hacemos esto, la vida de esa región urbana disminuye perceptiblemente. Es útil relacionar intuitivamente la geometría urbana con la “vida” -aunque este último término no se pueda definir con precisión- porque se siente su presencia inmediatamente. Como resultado de sus propiedades geométricas (que analizaré más adelante), las ciudades “arbóreas” modernas no están vivas en el sentido en que lo están las ciudades que mantienen una estructura más tradicional.
Alexander descubrió que una ciudad viva está modelada por una semi-trama matemática (es decir, una red), en contraste con una ciudad muerta, que está modelada por un árbol. Una red tiene un número mucho mayor de conexiones internas que un árbol de tamaño comparable. No sólo hay muchas conexiones en una red, sino que hay una gran variedad de ellas; por el contrario, los árboles tienen conexiones únicas. Sin embargo, me ha parecido más práctico dejar de lado la terminología de árbol y semi-trama y abordar el tema desde el punto de vista de los sistemas jerárquicos. Si consideramos que una ciudad viva es un sistema complejo coherente, ¿podemos descomponer dicho sistema en módulos? Resulta que pensar en este problema nos lleva a un razonamiento paralelo al del artículo de Alexander. Esto no es sorprendente, ya que Alexander, junto con Jane Jacobs (Jacobs, 1961), fue el primero en comprender la complejidad organizada de las regiones urbanas. Puedo intentar simplificar el mensaje de Alexander replanteándolo de la siguiente manera:
“Si se pueden segregar ordenadamente las funciones o las regiones en el plano de una ciudad, ésta representa un árbol y, en consecuencia, no está viva”.
Parcelas alternativas de una ciudad viva
Los teoremas de descomposición para sistemas complejos se publicaron por primera vez hace unos cuarenta años (Courtois, 1985; Simon, 1962; Simon y Ando, 1961). Voy a utilizarlos para intentar comprender la complejidad de la forma de las ciudades. Una ciudad viva se compone de partes, pero ¿cómo se determinan esas partes? La elección de los componentes básicos de un sistema complejo es en realidad arbitraria y depende del punto de vista del observador. Esto se debe a que el todo no es en absoluto reducible a las partes y su interacción. Se pueden definir subsistemas por comodidad, pero cada subsistema no se comporta de forma totalmente independiente. Para ayudar en mi análisis, una ciudad puede descomponerse de varias formas distintas; por ejemplo:
1. En edificios como unidades básicas (como se hace habitualmente) y sus interacciones a través de caminos conectivos.
2. Como un conjunto de caminos conectivos anclados y guiados por edificios (Salingaros, 1998).
3. Como espacios externos e internos conectados por caminos conectivos y reforzados por edificios (Alexander, 2001; Salingaros, 1999).
4. Como los bordes e interfaces que definen los espacios y las estructuras construidas (Alexander, 2001; Salingaros, 2000a).
5. En patrones de actividad e interacción humana que se producen en los bordes e interfaces urbanos (Alexander, Ishikawa et al., 1977; Salingaros, 2000b).
Son posibles otras descomposiciones, en las que se identifica un tipo diferente de unidad básica. Cualquier módulo que pueda utilizarse como bloque de construcción de un sistema complejo tendrá en sí mismo complejidad interna y no estará vacío ni será homogéneo. Esto nos permite construir la ciudad desde varias perspectivas totalmente distintas. Evidentemente, la forma de la ciudad resultante puede tener un aspecto radicalmente distinto en función de la elección del tipo de unidad básica que se utilice para construirla. Todas las opciones podrían ser igualmente válidas, y cada una de ellas conduce a una comprensión parcial de la complejidad de la forma y la función urbanas. Lo que quiero decir es que una ciudad viva es la superposición y el compromiso equilibrado entre todas estas opciones diferentes.
De las cinco alternativas de parcelación de una ciudad viva ofrecidas anteriormente, sólo el primer método es reconocible como parte del pensamiento urbanista estándar. Los otros cuatro, aunque son esenciales para un análisis matemático de la forma de la ciudad, siguen siendo descartados o considerados irrelevantes por la mayoría de los profesionales. La única manera de que los estudiantes aprendan sobre ellas es a través de los escritos de Alexander y sus colegas (Alexander, Ishikawa et al., 1977; Alexander, 2001) y Jan Gehl (Gehl, 1987), entre otros. No creo que sea posible diseñar o reparar entornos urbanos sin comprender a fondo cómo el espacio entre los edificios contribuye — de hecho, proporciona la base — a la “vida” urbana.
El primer enfoque (1) dispone los edificios en un cierto orden. Por desgracia, esto puede impedir la generación de conexiones útiles. La alineación geométrica suele sustituir, y en muchos casos reemplaza, las conexiones entre los nodos urbanos. El segundo enfoque (2) crea una jerarquía de vías, desde las vías peatonales protegidas hasta las autopistas. Cuando se construye una ciudad a partir de las vías peatonales, disponiendo los demás elementos urbanos de manera que no perturben la estructura de las vías, la organización de los edificios se vuelve más floja y menos simétrica. La geometría resultante es lineal y conectada; no es aleatoria ni caótica. Las ciudades históricas y los asentamientos ilegales obedecen a esta geometría mucho más libre. Sin embargo, empezar por las vías rápidas para construir una red conectada no funciona, porque invierte las prioridades de escala (Alexander, Ishikawa et al., 1977; Salingaros, 1998).
Módulos urbanos y fuerzas de conexión
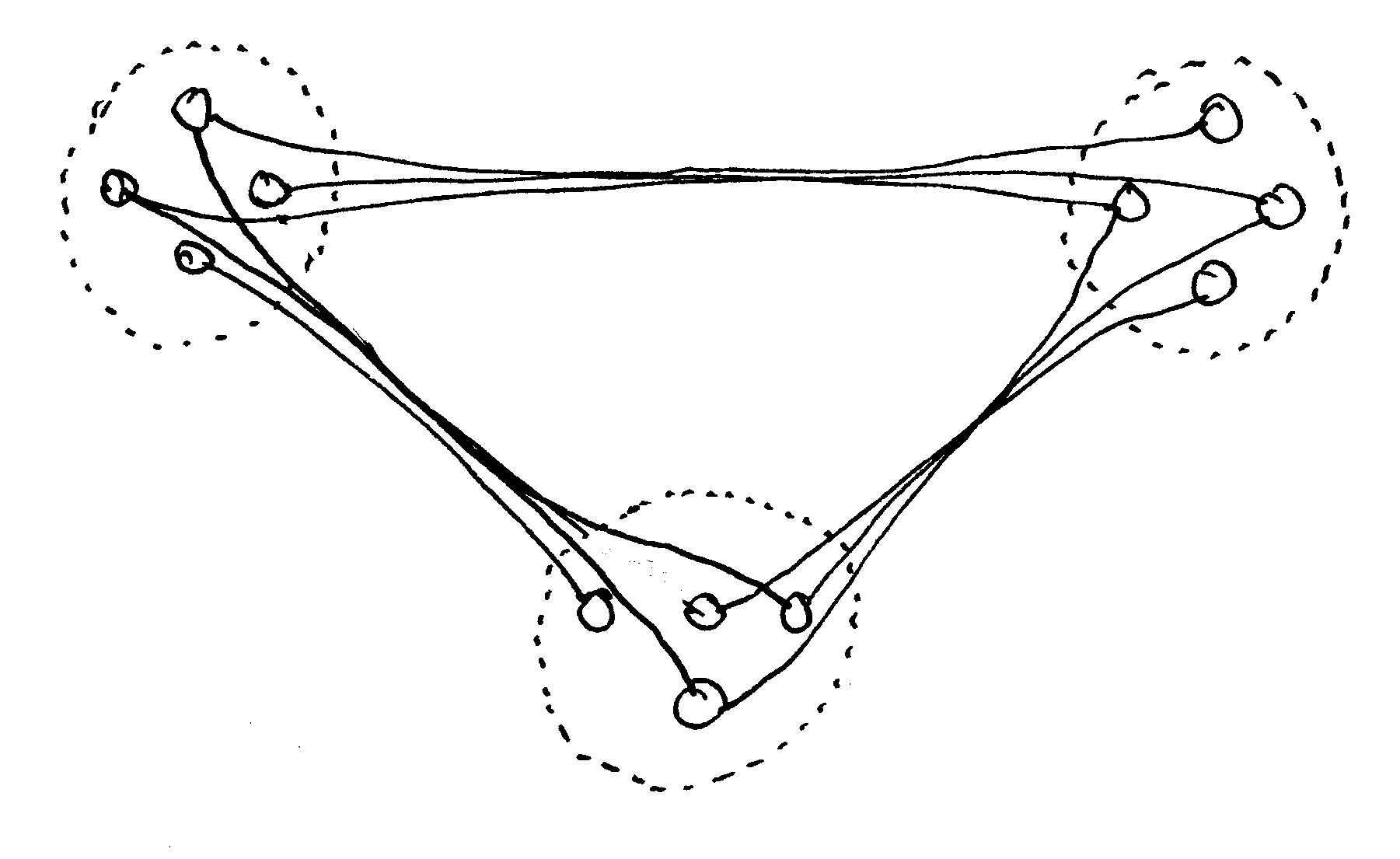
Un “módulo” es cualquier grupo de nodos (unidades) con un gran número de conexiones internas (Figura 1). Muchos de esos nodos también van a estar conectados a otras unidades fuera del módulo, siendo el propósito de definir un módulo el de internalizar conexiones relativamente fuertes. La modularización es un proceso de estabilización, ya que los buenos módulos contienen las fuerzas más fuertes para que los módulos (que son entidades más grandes) puedan interactuar entre sí más débilmente. Para hacer una analogía, imaginemos el movimiento térmico de las partículas: las más pequeñas vibran más rápido, mientras que los grupos más grandes vibran más lentamente porque tienen más inercia. Podemos entonces construir módulos de módulos, etc., según una jerarquía de fuerzas de fuerza decreciente.
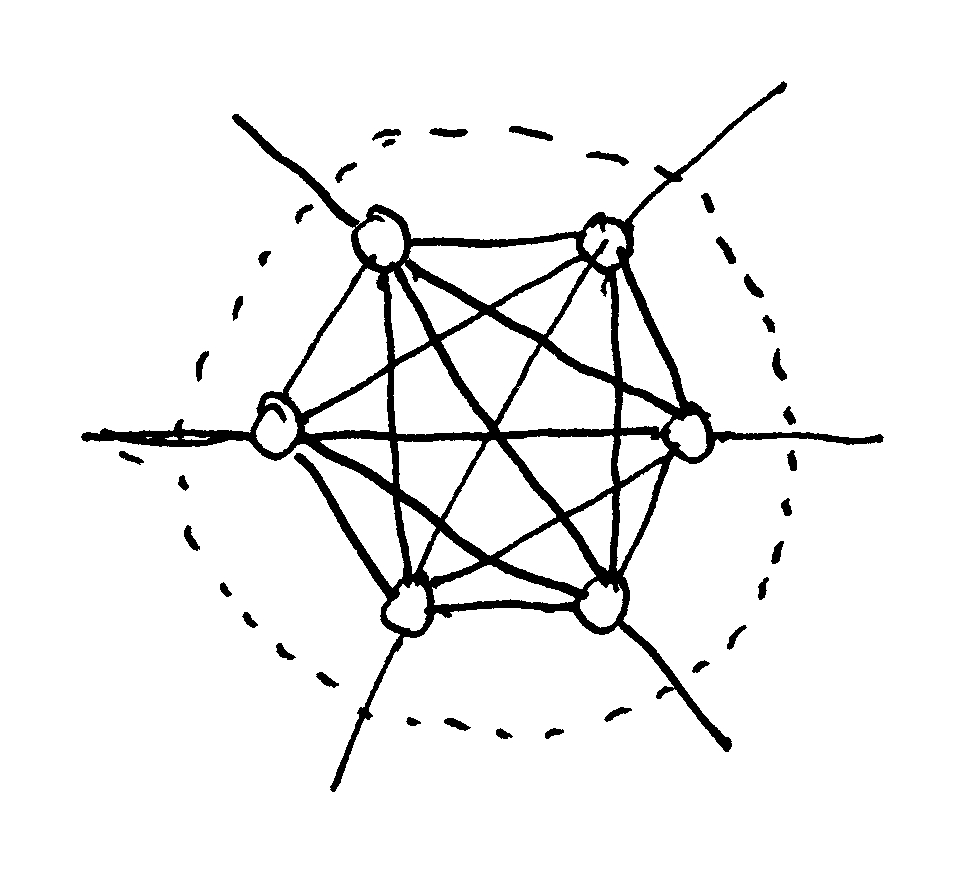
Los sistemas coherentes están definidos por unidades fuertemente conectadas, algunas de las cuales (aunque no necesariamente todas) pueden agruparse en módulos. Los elementos de un módulo no deben estar excesivamente separados entre sí, pero no son necesariamente adyacentes. El criterio no es la proximidad geométrica, sino la conectividad: las conexiones entre los nodos internos deben ser más fuertes que las externas. Así, un módulo urbano no tiene por qué tener un aspecto agradable en un plano; y a la inversa, una agrupación geométricamente regular de nodos no es automáticamente un módulo urbano. Un grupo de nodos sin conexión entre sí no formará un módulo (Figura 2).
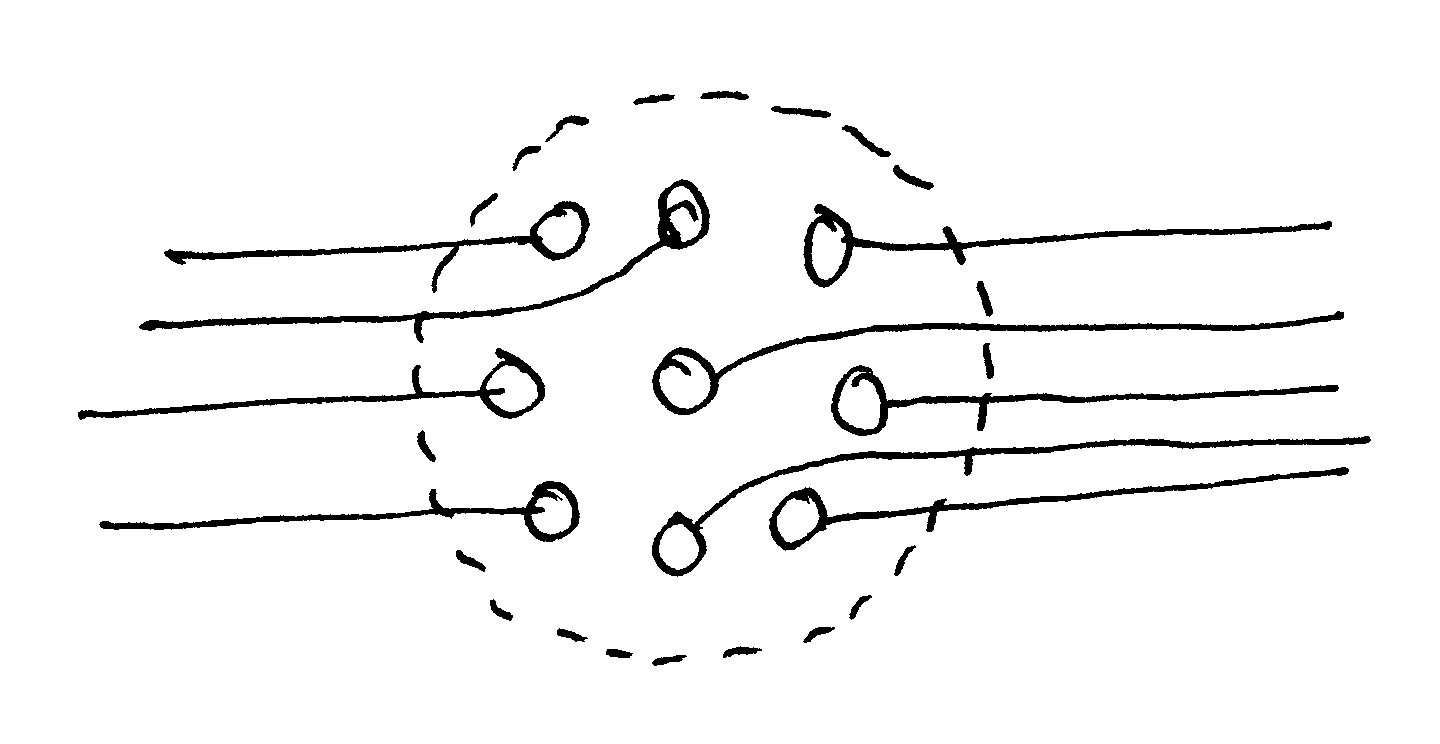
La conectividad puede consistir en la continuidad geométrica, la conectividad entre nodos o el intercambio de personas e información. Los edificios se acoplan geométricamente al tener paredes comunes; o bien se conectan a través de un espacio intermedio (Salingaros, 2000a). Este espacio puede contener recorridos e información que vinculen a los edificios que lo rodean. Una zona peatonal o plaza puede ser o no un elemento de conexión, dependiendo de si es muy utilizada o no. Eso, a su vez, depende de cómo se distribuyan los nodos en su periferia para que la gente necesite cruzar el espacio. Una plaza desolada y vacía no es un elemento conectivo como tampoco lo es un aparcamiento. Las conexiones de los senderos deben diseñarse para fomentar el libre intercambio de usuarios entre los nodos, y debe haber razones funcionales para este intercambio. Tampoco hay que descartar la conectividad informativa en el suelo, como ocurre cuando un patrón de suelo enlaza visualmente con las estructuras circundantes (Mikiten, Salingaros et al., 2000).
Una carretera muy transitada que separa los edificios es un límite que corta posibles caminos entre ellos (Salingaros, 1998). El interés informativo de las fachadas de los lados opuestos de una calle estrecha podría superar esta separación, a menos que el tráfico vehicular impida a los peatones cruzar. Este ejemplo subraya las funciones de apoyo mutuo de la conectividad informativa y del camino. Adoptar superficies lisas en edificios y pisos, y construir hasta los retranqueos suprime la conectividad informativa. El automóvil destruye el espacio peatonal al obligar a ensanchar las calles y hacer irrelevantes los diseños de las fachadas de los edificios y del suelo. Por otro lado, el papel positivo del automóvil es hacer accesibles los nodos urbanos. A menudo, una vía de poco tráfico que desemboca en una zona peatonal de difícil acceso mejora la conectividad del espacio urbano en lugar de dificultarla (Salingaros, 1999).
En cuanto comprendemos que una ciudad viva no se compone de edificios simplemente sentados uno al lado del otro, sino que la vida de una ciudad surge de su conjunto de conexiones, entonces la necesidad de que la geometría dé cabida a esas conexiones se vuelve primordial. Se empieza a pensar en configuraciones geométricas más complejas y entrelazadas que puedan soportar múltiples conexiones, y a fijarse en ejemplos urbanos del pasado que lo consiguieron (Salingaros, 2000a). Una parte esencial de esta imagen es permitir una multiplicidad de conexiones alternativas, ya sea a través de caminos conectivos o de información. Está claro que los atributos de una ciudad viva son
(i) la riqueza de la información, y
(ii) la priorización de las vías peatonales.
Estos requisitos no tienen por qué afectar a la red de conexiones vehiculares.
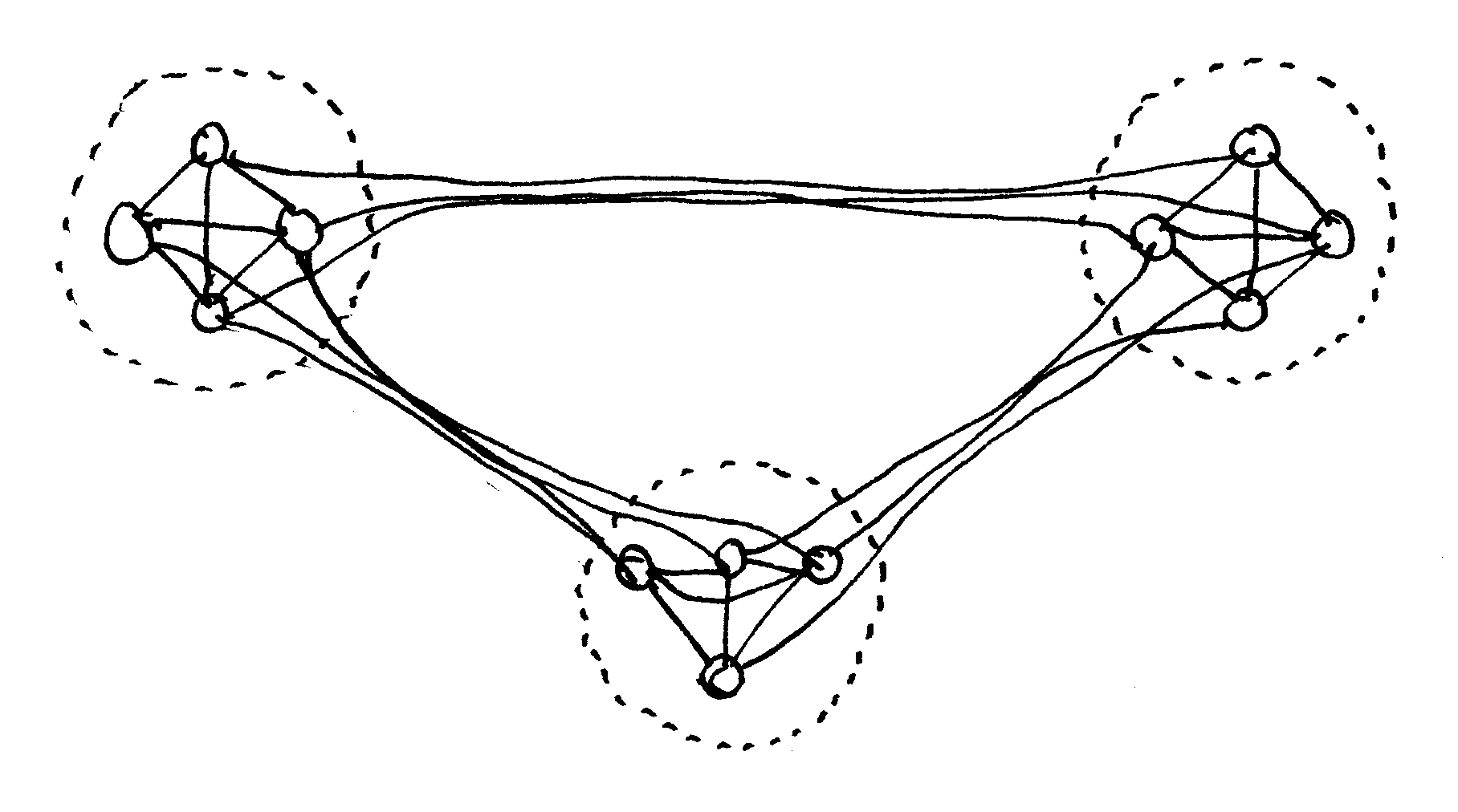
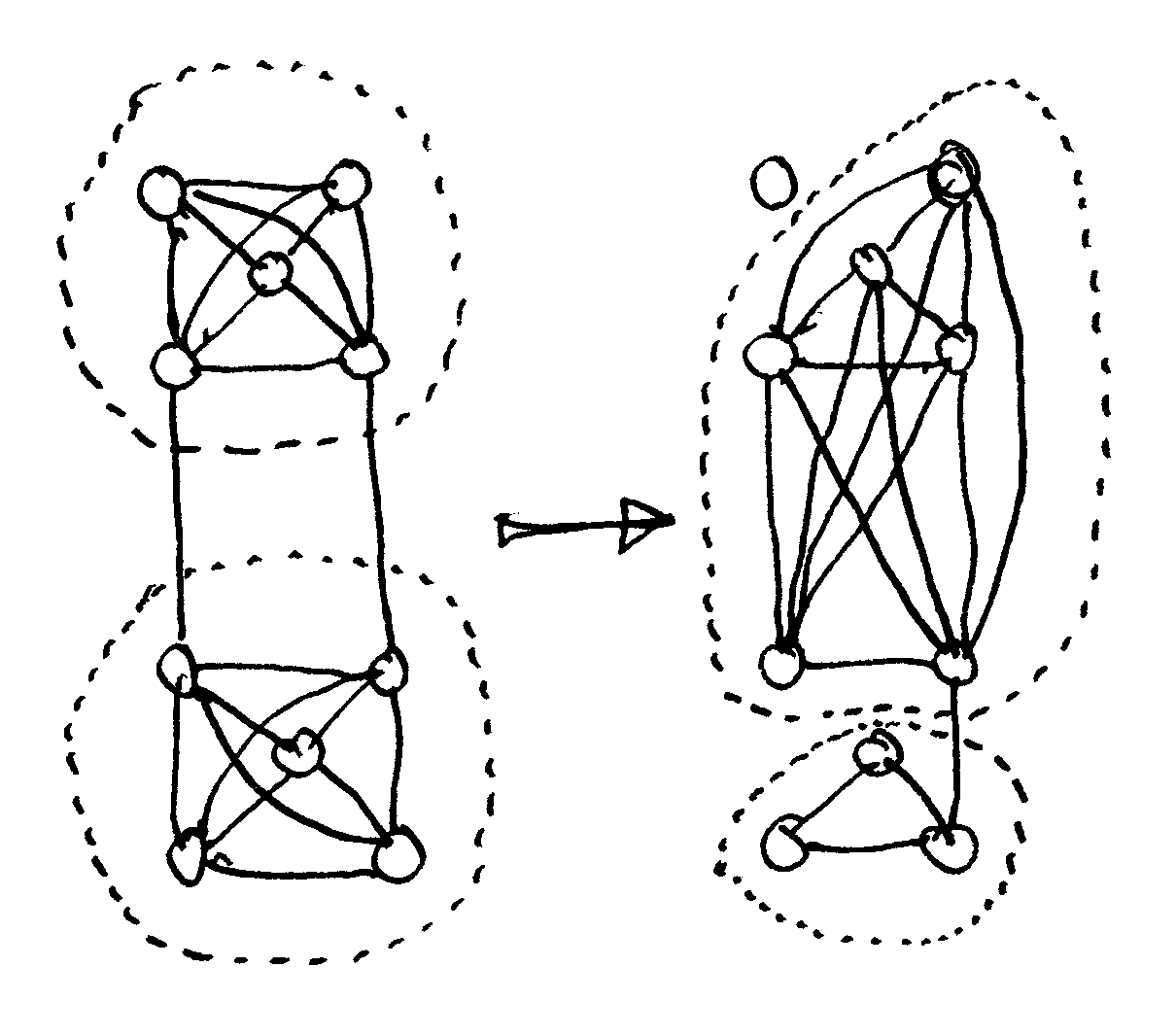
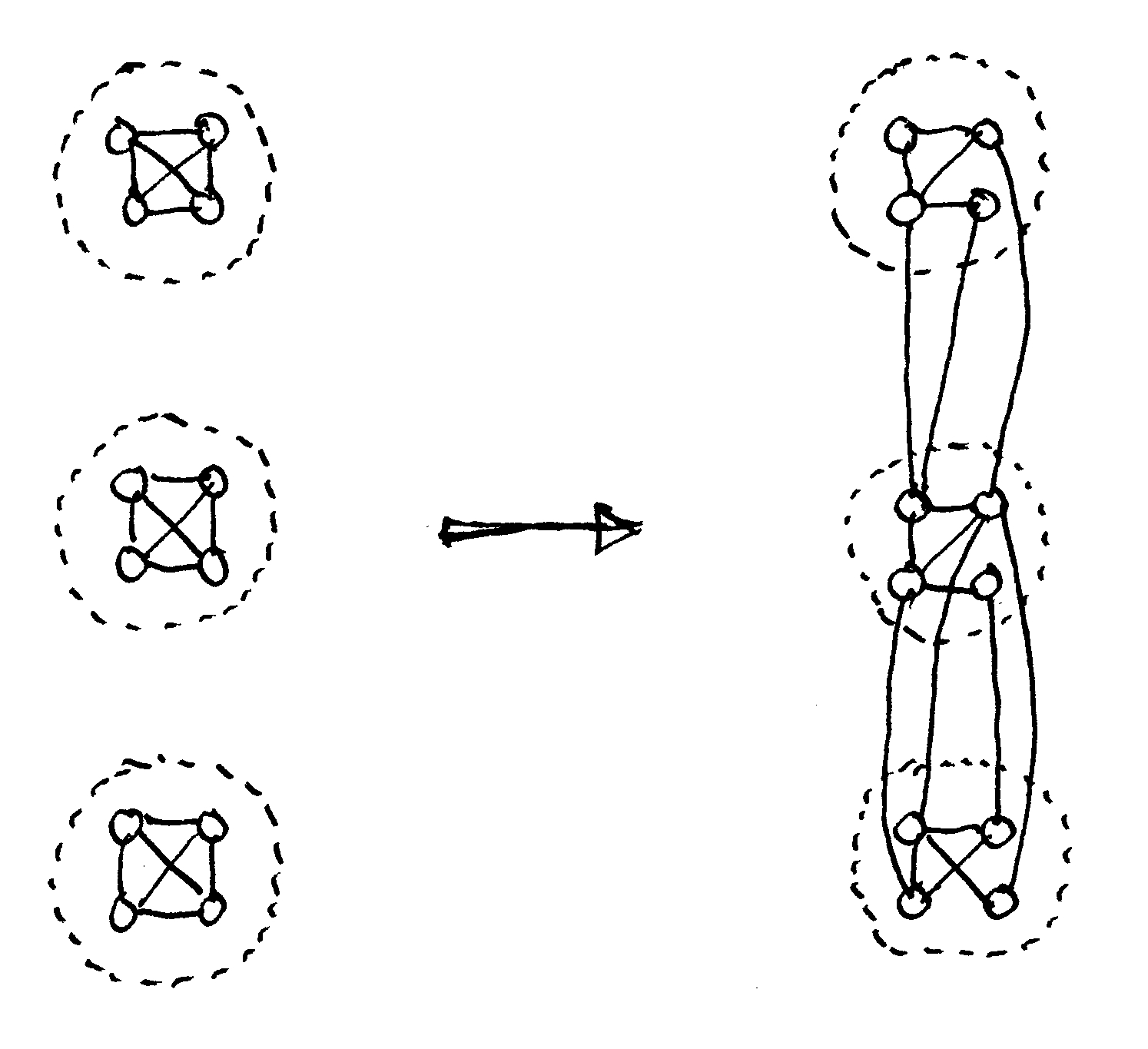
La unión entre módulos tendrá éxito si se produce a lo largo de una región que sea más débil que las conexiones internas de cualquier módulo; es decir, una unión debe separar el sistema donde haya vinculación o transición en lugar de una estructura concentrada. La parcelación sigue la fuerza relativa de las fuerzas de cohesión que definen un sistema: las fuerzas internas fuertes mantienen unido un módulo, mientras que las fuerzas más débiles mantienen los distintos módulos en su sitio dentro del sistema (Courtois, 1985). Aunque demasiado simplificado, el ejemplo de la figura 3 ilustra la contención de fuerzas dentro de los módulos: hay 3 enlaces inter-modulares en cada caso, mientras que cada módulo contiene 6 enlaces internos.
Módulos urbanos y alineación geométrica
Una vez establecida la noción de módulos urbanos en virtud de su conectividad interna, debemos disipar algunos malentendidos en la práctica urbanística de finales del siglo XX. El primero y más importante es la confusión entre conectividad y alineación geométrica. Una no implica automáticamente la otra; significativamente, hoy en día se gastan muchos esfuerzos y costes en la alineación geométrica, y el resultado perjudica la vida urbana. La simple alineación en las fases iniciales de la planificación no es un factor que contribuya a la coherencia urbana (Salingaros, 2000a). La alineación entra en juego como mecanismo de organización en un sistema urbano que funciona, y resulta útil cuando la coherencia surge de una subestructura que interactúa intensamente.
Para ilustrar lo que quiero decir, consideremos un ejemplo extraído del plano de una ciudad. Asumiré una geometría para los nodos y sus conexiones (a diferencia de los nodos simbólicos mostrados en las figuras anteriores). Los seis nodos mostrados en la Figura 4 podrían ser edificios de cualquier tamaño en una agrupación simétrica vista desde el aire, una situación muy común hoy en día. En la parte superior de la figura 4 vemos la simetría geométrica en el plano, que da la impresión engañosa de que existe alguna forma de ordenación urbana. La parte inferior de la figura 4 muestra dónde se encuentran realmente las conexiones entre los seis nodos: no es lo que uno espera de un grupo ordenado de seis nodos urbanos. Hubiera sido preferible un diagrama conectivo que relacionara los seis nodos con conexiones de corto alcance.
Aunque la figura 4 ilustra un ejemplo negativo, representa una situación mucho mejor que la existente en muchas regiones urbanas. Al fin y al cabo, los seis nodos mostrados en la figura 4 están en su mayoría conectados entre sí, aunque esas conexiones no sean muy prácticas. Gran parte de lo que se construye hoy en día entra en la categoría de “cerca pero desconectado”. Eso corresponde a tener los nodos mostrados en la parte superior de la figura 4 sin ninguna conexión entre sí (véase también la figura 2). Esta patología urbana debe entenderse como la ausencia de toda necesidad de comunicación entre los nodos distintos. Limitarse a proporcionar conexiones potenciales que quedan sin utilizar no puede construir una ciudad viva.
Un sistema urbano trata de autoorganizarse para desarrollar vínculos entre sus numerosos nodos. Un grupo de nodos estrechamente acoplados definirá un módulo urbano. El propósito del gobierno y de la legislación debe ser facilitar todas estas conexiones, en todas las escalas diferentes, y para todas las personas diferentes (es decir, la fuerza de trabajo, las personas con y sin coche, los ancianos, los niños, los discapacitados, etc.). Las fuerzas de conexión de las interacciones sociales empujan a la gente a utilizar los sistemas de peatones, autobuses, tranvías, trenes ligeros y ferrocarriles principales, además de los coches privados. Cada sistema de transporte definirá su propia geometría de red lineal, y requiere una infraestructura independiente. Es más económico a largo plazo fomentar sistemas de transporte múltiples y que compitan entre sí, en lugar de intentar empujar todas las conexiones hacia un único canal.
La alineación geométrica en las ciudades vivas no proviene de intentar satisfacer un ordenado plano aéreo rectangular, sino de facilitar la geometría de las redes de transporte superpuestas. La conectividad peatonal alinea los edificios. El exterior de los edificios proporciona el tejido construido que define los canales del flujo de transporte, ya sea para el coche, el autobús o el peatón. Esta es una ley fundamental del urbanismo, que se corresponde con nuestras parcelas (3) y (4) dadas anteriormente. Una ciudad se compone de “espacios externos e internos conectados por caminos y reforzados por edificios”, y de “bordes e interfaces que definen los espacios y las estructuras construidas”. A pesar de los trabajos anteriores de Hillier y Hanson (1984; 1997; 1999), de Gehl (1987) y de Alexander, Neis et. al. (1987) que apoyan esta ley, los planificadores siguen ignorándola. Existe una confusión fundamental sobre la necesidad de alinear los módulos urbanos y, en consecuencia, la conectividad urbana se resiente.
Fijémonos en la conectividad peatonal, que es la red de menor escala que une los nodos urbanos y sin la cual no puede haber vida urbana. Como se ha dicho en otro lugar (Salingaros, 1999), el espacio urbano está definido por regiones exteriores convexas que están parcial- — pero no totalmente — rodeadas por los muros exteriores de los edificios. Cada región del espacio urbano bien definida, por pequeña o modesta que sea, necesita estar conectada en una red de caminos peatonales, y este proceso linealiza y canaliza el espacio urbano. Hillier y Hanson (1984) determinaron precisamente esta estructura en un análisis detallado de los entornos peatonales vivos en muchas culturas urbanas diferentes. Correlacionaron el grado de vida social y comunitaria directamente con la intensidad de la red conectiva del espacio urbano.
En la sección 7, más adelante, se analiza cómo las redes de espacio urbano peatonal que funcionaban perfectamente (y que mantenían unidos los módulos urbanos) fueron sacrificadas en favor de los coches. Hoy en día, tenemos que entender que esta sustitución nos ha hecho olvidar por qué el flujo peatonal determinaba la alineación correcta de los nodos urbanos. Además, introdujo una geometría totalmente diferente, hostil al espacio urbano peatonal. La geometría de la red de automóviles no alinea los edificios. Tenemos aquí dos entidades contrapuestas: por un lado, una red urbana peatonal definida enteramente por la alineación de los muros exteriores de los edificios (es decir, su límite); y por otro, una red de automóviles definida directamente por sus caminos construidos (es decir, la superficie de la carretera). Para hacer las cosas más difíciles, las vías para automóviles invaden y borran el espacio urbano peatonal existente. La magnitud de este daño se ve agravada por la confusión sobre lo que realmente ocurre.
El malentendido se manifiesta cuando los planificadores tratan a los peatones como a los coches, trazando caminos geométricos que a nadie le gusta utilizar. Se espera que nos ciñamos a las vías peatonales de hormigón, como si se tratara de un juguete robótico (y los arquitectos hacen esfuerzos extraordinarios para obligarnos a ello). Sin embargo, por profundas razones psicológicas y fisiológicas, los peatones se aferran a los límites construidos y toman el camino recto más corto hacia un nodo urbano visible, por lo que cualquier camino funcional tiene que seguir las necesidades humanas (Salingaros, 1998).
La gente ignorará los caminos no naturales que algún planificador bienintencionado pero ignorante haya trazado, y cortará sus propios caminos a lo largo de las paredes y a través del espacio urbano peatonal protegido, exactamente donde los límites construidos y los objetivos visuales definen el camino. Esto puede ponerlos en peligro por los automóviles y los cambios de nivel. Los espacios urbanos históricamente exitosos, y los caminos peatonales en general, sólo se dan en aquellos casos en los que los exteriores de los edificios se doblan y cooperan para definir el ámbito peatonal. Los espacios urbanos son espacios abiertos peatonales que albergan una multitud de caminos entrecruzados (Salingaros, 1998).
Para subrayar el contraste entre la geometría del movimiento peatonal y la de la ciudad del automóvil, mostraré cómo la primera crea alineación, mientras que la segunda promueve la aleatoriedad. Este resultado es inesperado para la mayoría de los lectores, ya que es lo contrario de lo que afirmaban las autoridades de planificación en el siglo XX. La figura 5 muestra cómo los muros exteriores cooperan para unir los espacios urbanos, junto con sus edificios de apoyo, en un módulo urbano. Supongo que este conjunto protege la continuidad del espacio urbano peatonal, con la posibilidad de que los coches lo atraviesen de forma controlada, pero sin amenazar a los peatones. Una condición absoluta es que los coches no saturen el espacio urbano aparcando. El resultado es una ordenación geométrica en una cuadrícula deformada, ya que la red urbana linealiza (es decir alinea) los nodos construidos. No es la ordenación la que crea las conexiones, sino al revés.
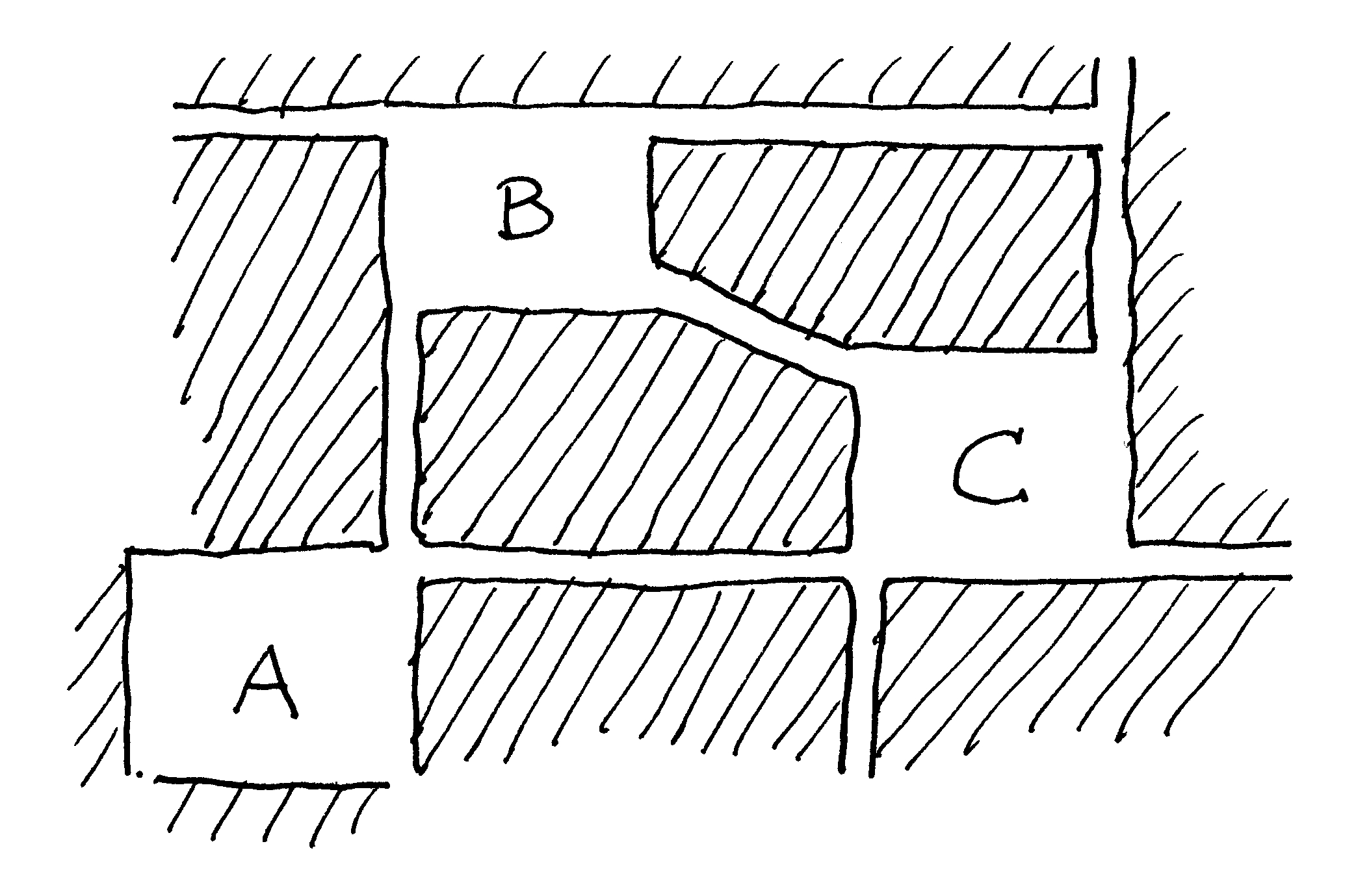
La figura 6 muestra la geometría de la ciudad del automóvil. Los nodos son aparcamientos. Los edificios no definen ningún orden geométrico concreto, ya que no existe ningún principio de ordenación. Los edificios sólo necesitan tener una entrada en el aparcamiento. Si dos edificios cercanos están alineados de alguna manera, es una decisión puramente arbitraria de sus arquitectos. La geometría no tiene nada que ver con la conectividad. Como los coches pueden ir a cualquier lugar donde exista pavimento, y no se cansan como los seres humanos, sus trayectorias pueden desarrollar una geometría amorfa. A gran velocidad, las carreteras se vuelven rectas. Lo que he mostrado es un “árbol” en la terminología definida anteriormente. En la ciudad contemporánea, hay que tomar la autopista para ir de un nodo urbano a otro. En el tejido urbano más antiguo de la posguerra, también habrá conexiones locales (normalmente sólo para coches) entre los nodos de aparcamiento. Sólo en tejidos urbanos mucho más antiguos la conectividad y el flujo peatonal influyen en la geometría de los nodos urbanos.
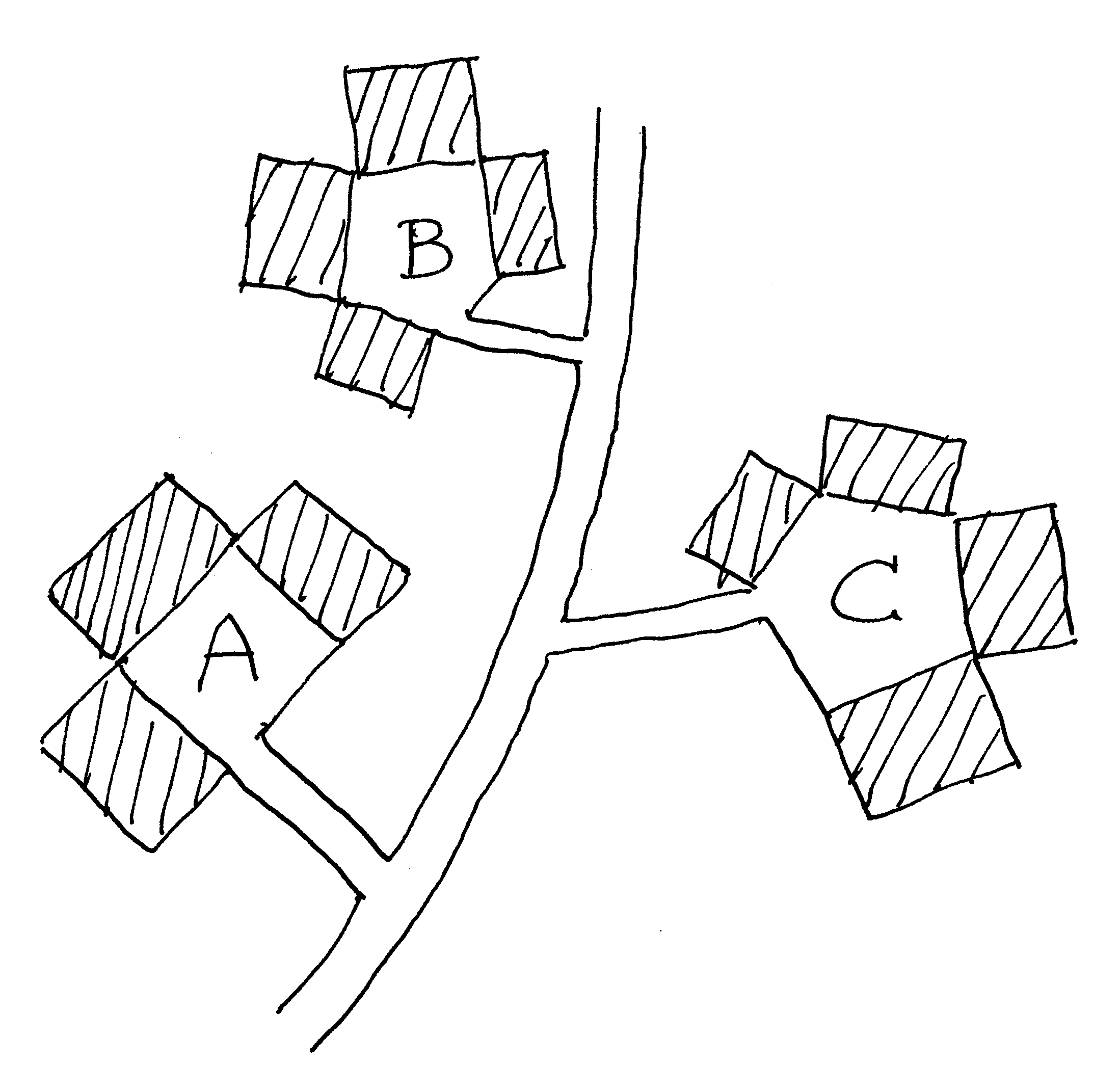
La homogeneización y la segregación destruyen la estructura del sistema
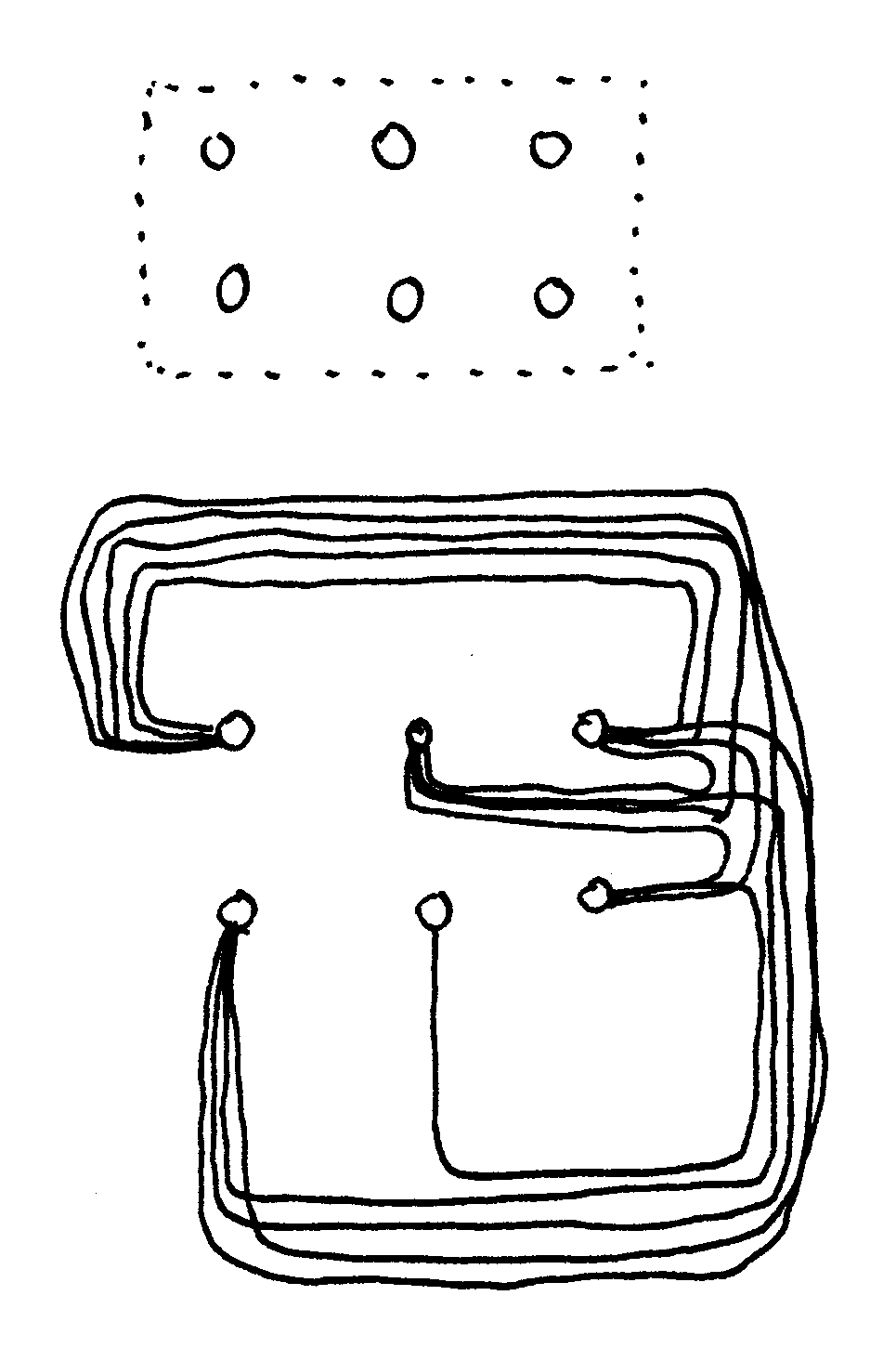
Las normas de planificación que concentran los nodos que no interactúan impiden que se formen módulos urbanos. Al negar la base de la coherencia de un sistema urbano, es matemáticamente imposible realizar una ciudad viva. Las ciudades contemporáneas imponen un conjunto de leyes de zonificación que generan una estructura física muy particular: vastas regiones urbanas con sectores homogéneos y mucho movimiento mecánico por todas partes, pero con muy poca vida. En el ejemplo de la figura 7, tres no-módulos (cada uno de ellos formado por cuatro nodos adyacentes pero no conectados) se enlazan entre sí. La patología de esta situación se ve al comparar los enlaces: 3 enlaces externos, pero 0 enlaces internos en todos los casos.
La concentración de funciones similares como en el ejemplo de la figura 7 viola la composición básica de un sistema: las conexiones internas de un módulo deben ser más fuertes que las conexiones que forman la interfaz entre los módulos (Courtois, 1985; Simon, 1962; Simon y Ando, 1961). Dado que las unidades similares no suelen interactuar entre sí, intentar agrupar unidades del mismo tipo en un módulo carece de sentido. En lugar de reducir las fuerzas que actúan entre los módulos, tal agrupación externaliza todas sus fuerzas. La parcelación modular sólo es eficaz cuando las fuerzas más fuertes están contenidas dentro de los módulos. La contención de las fuerzas mediante el acoplamiento de las unidades que interactúan fuertemente en los módulos suele dar lugar a una partición geométrica no evidente.
Alexander señala en “A City is Not a Tree” que el diseño del entonces nuevo Lincoln Center de Manhattan es fundamentalmente defectuoso (Alexander, 1965). La segregación de los edificios de artes escénicas en una región no tiene sentido porque no tienen caminos conectivos. Por caminos me refiero a conexiones reales que satisfagan la necesidad humana de ir de un punto a otro, lo que tiene muy poco que ver con el lugar donde se construyen realmente los “senderos” de hormigón (Salingaros, 1998). Los edificios están desconectados en el sentido de la parcelación (2) antes mencionada (véanse las figuras 2 y 7). ¿Se acercará alguien a escuchar una sinfonía en el edificio de al lado después de haber ido primero a la Ópera? No es probable. No hay caminos conectivos y, por tanto, no hay conexiones humanas entre los distintos edificios del conjunto.
Dualidad entre los edificios y el espacio urbano
La división de un sistema en componentes puede llevarse a cabo mediante una interfaz adecuada. Las interfaces entre los módulos que componen un sistema complejo deben ser en sí mismas complejas; tienen que acoplar y conectar, además de separar las distintas unidades. Un sistema puede descomponerse parcialmente en un conjunto de módulos complejos semiautónomos e interfaces igualmente complejas que permitan su unión. Así es precisamente como ocurre en la biología. El éxito de la descomposición del sistema depende de la correcta distinción entre módulos e interfaces. No identificar las interfaces correctas impide que el sistema funcione después de la parcelación. Las conexiones a nivel de sistema en la descomposición modular requieren que se permita una complejidad suficiente en una interfaz.
En “A City is Not a Tree” (Alexander, 1965), Alexander identifica sus unidades básicas como nodos geométricos. Cada uno de ellos podría representar un edificio o cualquier punto fijo del espacio urbano. A continuación, Alexander basa su análisis en la estimación del enorme número de conexiones necesarias para que esas unidades definan una ciudad viva. Llega a la conclusión de que la práctica urbanística del siglo XX no contempla — y sus principios teóricos ni siquiera admiten la existencia — el número necesario de conexiones. Además, permitir conexiones alternativas que permitan a un sistema generar su propia complejidad contradice la idea de la planificación, que supuestamente tiene que prever completamente todas las conexiones. Dos nodos cualesquiera de un árbol matemático están conectados por un único camino, por lo que una ciudad “arbórea” encaja en esta mentalidad.
Mi enfoque aquí es más general, ya que concibo los distintos tipos de interfaces como los módulos de una ciudad viva. Por ejemplo, una interfaz geométrica a lo largo de la cual se mueven las personas, y dentro de la cual éstas interactúan y realizan funciones que hacen que las ciudades estén “vivas”, constituye un módulo. Sus unidades son caminos combinados en lugar de edificios. Estos módulos están unidos en una red. Este objeto tiene un aspecto orgánico y fractal; se parece vagamente a alguna extraña forma vegetal. Las conexiones determinan las formas de los edificios y no al revés. Se trata de una inversión de la figura y el suelo en el plano de una ciudad: ¿los espacios exteriores contribuyen a construir el tejido urbano, o están completamente ocupados por los automóviles? Alexander (Alexander, 2001) se ocupa precisamente de todas esas conexiones.
Las ciudades antiguas se construían diseñando un espacio urbano continuo en toda la ciudad, como en nuestra tercera parcelación (3) (Alexander, 2001; Gehl, 1987; Salingaros, 1999). Esta era una forma obvia de hacer las cosas mientras el movimiento peatonal era el medio de transporte dominante en las ciudades: las principales funciones urbanas se producían en el espacio urbano propiamente dicho. Ese planteamiento tuvo que ser revisado para dejar entrar a los coches en número creciente, que por su tamaño y velocidad dominantes desplazan a los peatones y a las conexiones peatonales. Sin embargo, es evidente que los planificadores modernistas fueron demasiado lejos al disolver por completo el espacio urbano y luego cortar autopistas a través de los núcleos de las ciudades. La importancia del espacio urbano se perdió en el siglo XX cuando el énfasis filosófico en las estructuras de significado pasó del espacio entre los edificios a la pura geometría de los edificios aislados.
La parcelación (4) construye una ciudad en términos de acoplamientos geométricos básicos en lugar de edificios aislados. Las interfaces geométricas son las unidades activas de la ciudad, pero sólo si consiguen acoplar los objetos de ambos lados (Salingaros, 2000a). Las interfaces son bordes que representan elementos lineales, a lo largo de los cuales se genera la “vida” de una ciudad. Sin embargo, en una región urbana típica construida hoy en día, todos los componentes geométricos están desconectados, por lo que no hay ningún borde interactivo. Lo cierto es que hemos olvidado cómo crear una interfaz conectiva. El acoplamiento casi siempre funciona a través de una región intermedia — el borde complejo, poroso o enrevesado — que se elimina hoy en día por razones estilísticas. Los bordes no conectados cumplen una función puramente decorativa.
Alexander y sus colegas se dieron cuenta de la importancia de las parcelas numeradas (4) y (5), y las utilizaron ampliamente al escribir “A Pattern Language” (Alexander, Ishikawa et al., 1977). Mediante el estudio de los ejemplos de estructuras urbanas más exitosas desde el punto de vista funcional y emocionalmente atractivas de la historia y de todo el mundo, descubrieron que los bordes conectivos desempeñan un profundo papel en la vida urbana. Muchos patrones de actividad humana se producen únicamente a lo largo de interfaces geométricas, siendo el catalizador la complejidad de la propia interfaz (la parcelación (5)) (Salingaros, 2000b). El modernismo elimina deliberadamente la interfaz entre los elementos urbanos en la búsqueda de un estilo visual “puro” que no muestre conexiones. Por esta razón, muchos patrones alejandrinos parecen estar fuera de lugar en el canon del diseño urbano actual y, al ser incomprensibles, son ignorados.
El control y la supresión del surgimiento
Un sistema complejo del que se espera que responda a las condiciones internas cambiantes — como por ejemplo al diagnosticarse a sí mismo y corregir los daños internos — necesita estructuras emergentes. La autoestabilización, la reparación y la evolución son propiedades que no dependen de los módulos individuales, por lo que deben existir fuera de cualquier descomposición modular. Como las propiedades emergentes son globales, también están fuera de las funciones programadas originalmente y no pueden definirse a nivel modular. En este sentido, son “no funcionales” porque no se corresponden con las funciones originales diseñadas. Las conexiones emergentes sólo son posibles en un sistema que ya está muy conectado y que ofrece un mecanismo de conexiones adicionales.
Son precisamente estas propiedades evolutivas las que generan la vida biológica en un organismo; la inteligencia en el cerebro; así como la “vida” en un edificio o región urbana. Para fomentar la formación de propiedades emergentes, no podemos aplicar una única parcelación al entorno construido. En todos los sistemas, el surgimiento se produce desde nuevas conexiones y no estrictamente de las contenidas en los propios módulos originales. Mientras que los módulos son inicialmente fijos, pueden surgir conexiones adicionales de forma espontánea a partir de las interfaces entre módulos. En el cerebro humano, la multitud de conexiones neuronales trabajan conjuntamente para producir la conciencia, una propiedad que no puede entenderse a partir de los componentes del cerebro por sí solos (Edelman y Tononi, 2000).
La comparación entre un agregado simplista y un sistema con propiedades emergentes tiene que ver con la elección: el primero se prefiere en situaciones en las que todo tiene que estar totalmente controlado; mientras que el segundo se da en situaciones en las que el crecimiento espontáneo no es una amenaza. En el urbanismo, el contraste entre las regiones muertas y las vivas es muy marcado. Las ciudades muertas están planificadas de forma rígida para que no se permita la interacción espontánea entre las personas; los edificios concentran las unidades de oficinas o de vivienda en vertical para que se pueda controlar fácilmente una sola entrada; los complejos de apartamentos suelen estar controlados por una sola puerta; los centros comerciales interiores tienen entradas limitadas y vigiladas; etc. El control se impone además por medio de la legislación: no se puede merodear en público; no se puede caminar por la calle; no se puede sentarse en las paredes; no se puede comerciar en los enclaves residenciales; no se puede vender en la acera; etc.
Las ciudades vivas, en cambio, son más desordenadas geométricamente y contienen múltiples vías que ofrecen rutas alternativas tanto a los peatones como a los coches. Los edificios tienden a estar entrelazados y no demasiado dispersos, con usos mixtos y un número razonablemente pequeño de plantas. Los complejos de edificios se componen de edificios más pequeños conectados con múltiples entradas, en lugar de concentrarse verticalmente en un único edificio gigante. También encontramos aquí una proliferación de elementos urbanos “no funcionales” como pequeños parques, muros bajos, bancos, vendedores ambulantes, cafés en las aceras, quioscos, etc. Este entrelazamiento vital del comercio con la vida cotidiana, el paso del tiempo con extraños y la socialización en público proporciona los fundamentos dinámicos de la vida en una ciudad. El antiguo mercado o ágora no sólo era un centro de comercio, sino que era al mismo tiempo un centro de socialización e intercambio político e intelectual.
Las ciudades evolucionan con su propia forma
La zonificación conjunta de unidades que no interactúan crea no-sistemas patológicos, como centros comerciales funcionalmente concentrados y suburbios residenciales homogéneos (Salingaros, 2000a). Como es necesario vincular fuertemente estos dos grupos para la comunicación y el transporte, las conexiones de largo alcance generan enormes fuerzas externas que acaban provocando la asfixia funcional de las ciudades. La nueva situación genera a su vez nuevas configuraciones en la estructura urbana, que la planificación puede orientar en sentido positivo o negativo. Si se les deja solos, los ciudadanos intentarán reubicar sus negocios o su residencia en respuesta a las fuerzas urbanas.
Las conexiones responsables de los fenómenos emergentes surgen al tener muchas opciones alternativas que conectan un subsistema con otro. La posibilidad de elegir depende tanto de la geometría urbana como de la legislación. La posibilidad de elegir no existe cuando todos los nodos se conectan a través de un único camino. El surgimiento, y por tanto la evolución, son imposibles en una ciudad totalmente planificada que no ofrece ninguna elección entre las posibles alternativas. La evolución del sistema genera conexiones que cruzan tanto los límites modulares como las distintas escalas para conectar un subsistema con una estructura mucho más grande o mucho más pequeña: tales conexiones son extramodulares. Otras conexiones del sistema se reordenan o se cortan. Para entender la evolución de la morfología urbana, tenemos que examinar cómo una ciudad cambia sus conexiones a lo largo del tiempo.
Cualquier división de una ciudad en módulos — incluso si esos módulos tienen más sentido tanto estructural como funcionalmente — tendrá que basarse en el estado de la ciudad en ese momento concreto. Sin embargo, sabemos que las funciones y los nodos de una ciudad siempre cambian. Los sistemas tienen un orden más o menos jerárquico, en el que los componentes más pequeños que interactúan se asocian a componentes más grandes (pero no necesariamente encajan en ellos). Los componentes más pequeños se modifican continuamente o son sustituidos por otros componentes, lo que altera la composición interna de los módulos. Las interfaces que se encargan de las conexiones del sistema se ven modificadas por estos cambios. Habrá que dar cabida a nuevas conexiones que representen fenómenos emergentes; no se puede decidir de antemano cómo hacerlo.
El enfoque opuesto a la planificación segregada se intentó en las no tan recientes Ciudades Nuevas, que están formadas por un conjunto de pueblos artificiales. Esta parcelación tampoco funciona muy bien. Estas ciudades ideales parecen más humanas sobre el papel, porque sus módulos se basan en prototipos antiguos que funcionan. También siguen las leyes del sistema al estar descompuestas en módulos autónomos, cada uno de los cuales consta de unidades fuertemente acopladas, como casas, tiendas, escuelas, parques, etc. Alexander ya señaló que esta estructura es un árbol y, por tanto, no está viva (Alexander, 1965). La razón de ello es más sutil que en el caso de la ciudad modernista funcionalmente segregada, y tiene que ver con las fuerzas emergentes entre los módulos.
Una ciudad ideal construida a partir de módulos de aldea que no interactúan empezaría a deshacerse inmediatamente. La gente encontrará empleo en un módulo diferente; otros se trasladarán a otro módulo pero mantendrán a sus amigos, parientes y compras en su módulo anterior; los comercios cambiarán para que la gente vaya fuera de su propio módulo; una escuela vecina que se deteriora o simplemente el deseo de una mayor calidad obliga a una familia a enviar a sus hijos a la escuela de otro módulo; etc. Las fuerzas sociales y comerciales cortan las conexiones internas y generan nuevas y fuertes conexiones entre los módulos y fuera de ellos. La descomposición del sistema, cuidadosamente planificada, se deshace, haciendo inaplicable la partición original a gran escala en módulos. El sistema se degrada porque no está diseñado para dar cabida a las conexiones emergentes.
La distribución de las longitudes de los conectores
Es extremadamente difícil, si no imposible, planificar una ciudad viva de una vez. No nos queda más remedio que pasar de una planificación rígida impuesta a la estructura urbana a un proceso dependiente del tiempo que guía la evolución natural de una ciudad. Alexander (Alexander, 2001) analiza cómo la geometría de una ciudad viva evoluciona con el tiempo. En este trabajo, he tratado de indicar los dos puntos extremos opuestos a partir de los cuales una ciudad trata de evolucionar: (A) el no-sistema zonal segregado con sólo conexiones de largo alcance; (B) el grupo utópico de aldeas artificiales que sólo tienen conexiones de corto alcance. Una ciudad viva se encuentra en algún punto intermedio entre estos dos extremos rígidamente planificados, aunque mucho más cerca de (B) que de (A). Además, la viabilidad de una ciudad depende de la libertad para reorganizar sus conexiones a lo largo del tiempo.
Estos dos modelos conectivos extremos para una ciudad se caracterizan por sus longitudes de conexión mutuamente excluyentes. ¿Cuál es la distribución óptima de las longitudes de conexión en una ciudad viva? Un resultado matemático sobre la distribución de tamaños (Salingaros y West, 1999) responde a esta pregunta. Los sistemas dependen de componentes de diferentes magnitudes, y la distribución de esas magnitudes es óptima cuando obedecen a una regla de escalado de potencia inversa. Esta regla de escalado dice que el número de conexiones de cada longitud es inversamente proporcional a su longitud elevada a una potencia entre 1 y 2. Por lo tanto, las conexiones cortas son mucho más comunes que las largas, y cuanto más larga sea la conexión, menos frecuente debería ser (Figura 10).
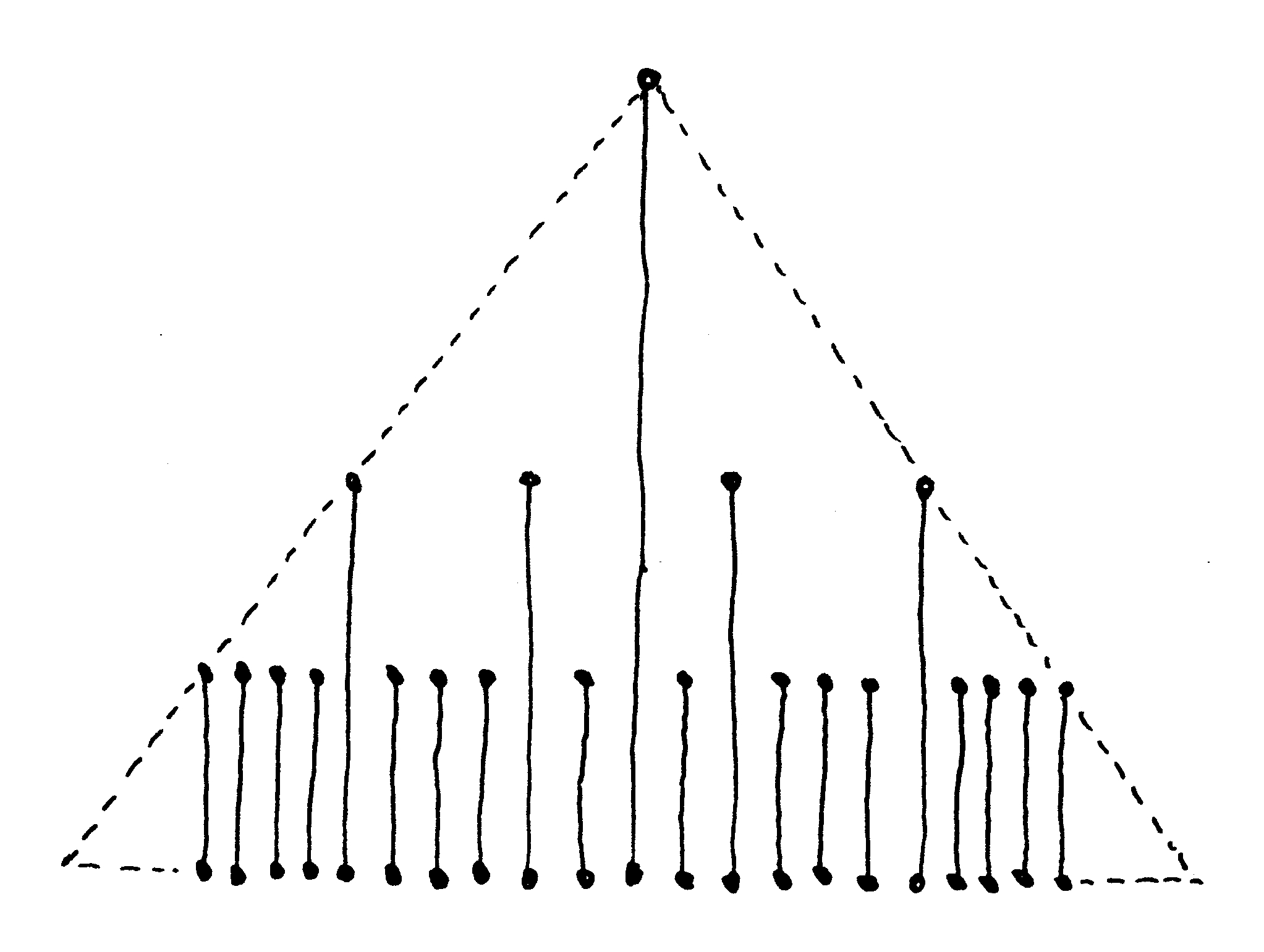
Un tejido urbano que funciona — barrios vivos que se conectan de forma mutuamente beneficiosa entre sí, así como con regiones urbanas distintas — contiene longitudes de conexión que obedecen a una distribución de potencia inversa. Volviendo a la dualidad entre nodos y conexiones comentada en un apartado anterior, la regla del poder inverso se aplica también a la distribución de los espacios urbanos. Los espacios urbanos tienen que estar destinados a grupos de personas en número creciente: muchos apropiados para grupos pequeños de personas, y sólo unos pocos que puedan albergar a muchas personas. El objetivo es fomentar las interacciones personales según la misma distribución: muchos contactos diarios íntimos o breves de pequeños grupos de personas en el espacio urbano, con disposiciones para la congregación menos frecuente de grupos más grandes.
El apoyo a esta conclusión proviene de una increíble variedad de sistemas complejos que obedecen la regla de escalamiento mencionada, desde la estructura del ADN, hasta las leyes de potencia de la economía, pasando por todas las formas fractales (Salingaros y West, 1999). La escala de potencia inversa es omnipresente en la naturaleza y se encuentra en una amplia gama de fenómenos tanto naturales como artificiales. La distribución de enlaces en la World-Wide Web sigue esta regla (Albert, Jeong et al., 1999). Quizá el ejemplo más relevante tenga que ver con la distribución de la longitud de las neuronas en animales invertebrados simples (Watts y Strogatz, 1998). La naturaleza ya ha resuelto el problema de cómo conectar los nodos de un organismo complejo de forma óptima. Existe una estrecha relación entre la escala de potencia inversa y las redes de “mundo pequeño”, cuyos detalles describiré a continuación.
La distribución de la longitud de las conexiones desempeña un papel fundamental en el funcionamiento de una red totalmente conectada. Las redes que aparecen tanto en los sistemas naturales como en los artificiales se sitúan entre dos extremos: (A) Redes aleatorias caracterizadas por enlaces aleatorios; y (B) Redes regulares que consisten sólo en enlaces de vecino más cercano (Watts y Strogatz, 1998). En las primeras, las longitudes de las trayectorias se agrupan en torno a una media de distribución, por lo que la mayoría de los enlaces son mucho más largos que los de los vecinos más cercanos. La reconexión de un sistema del tipo (A) mediante la desconexión de muchos enlaces largos y su sustitución por conexiones de longitudes cercanas; o la prolongación de algunas de las conexiones inicialmente cortas en (B) para generar conexiones medias y largas da lugar a una red de “mundo pequeño”, que tiene propiedades de conectividad muy mejoradas con respecto a las redes aleatorias o regulares (Watts y Strogatz, 1998).
Las distribuciones de potencia inversa caracterizan a los sistemas que no tienen una escala fija, es decir, que funcionan igual de bien en todas las escalas (Salingaros y West, 1999). En la práctica, las distribuciones de potencia inversa tienen un corte inferior en alguna longitud mínima permitida, que es el enlace del vecino más cercano, y su longitud media es algún múltiplo (entre 3/2 y 2) de la longitud más pequeña. Esto favorece las longitudes de conexión más pequeñas. En cambio, la longitud característica o media de una distribución aleatoria es una fracción (aproximadamente 1/3) del tamaño de todo el sistema, lo que representa la máxima longitud posible. Dado que la ciudad y el suburbio modernistas carecen de conexiones de pequeña longitud, la zonificación monofuncional empuja la longitud característica de las conexiones urbanas más allá de la media aleatoria, y más cerca de la distancia máxima.
Ecosistemas y geometría
Las ciudades pueden aprender de la modelización teórica de los ecosistemas. Los ecosistemas biológicos son complejos sistemas superpuestos compuestos por módulos de organismos de diferentes tamaños. Tiene tanto sentido definir un hábitat rectangular para algún animal como un “sector de vivienda”. Aislar plantas y animales en sus propios sectores segregados destruye un ecosistema. Una geometría de grano fino que permita la mezcla es un requisito previo para la vida. Podemos crear un arrecife artificial vertiendo coches viejos y frigoríficos en el fondo del mar; en pocos años está repleto de vida marina. Un lago cristalino de montaña (que ocupa un lugar destacado en nuestra lista según el valor estético) está esencialmente muerto, mientras que un estanque verde opaco lleno de troncos y ramas en descomposición suele ser rico en formas de vida.
Además de la geometría, entre las cualidades urbanas descuidadas están la evolución dinámica y la estabilidad. Los ecosistemas son dinámicos en el sentido de que su composición interna y sus límites cambian continuamente. Nadie planea un ecosistema, pero una intervención equivocada (ya sea por parte de los humanos o por eventos naturales catastróficos) puede destruirlo para siempre. La estabilidad de los ecosistemas se basa en la existencia de módulos de distintos tamaños: cada uno reacciona de forma diferente a las perturbaciones. Un modelo sencillo muestra que los módulos ecológicos grandes reaccionan más lentamente a las perturbaciones, mientras que los pequeños lo hacen más rápidamente. Esta diversidad incorporada garantiza cierta estabilidad básica ante distintos tipos de perturbaciones.
Una ciudad necesita el mismo tipo de resistencia a las condiciones cambiantes que tiene un ecosistema sano. No sé cómo diseñar esto, pero está claro que la solución debe venir de un conjunto de leyes urbanas — aún por derivar — que permitan a una ciudad evolucionar su propia vida, y mantenerla a lo largo del tiempo. No sólo hay que legislar las condiciones de la “vida” urbana en un conjunto de directrices que ayuden a la cohesión del tejido urbano, sino que las leyes deben guiar la evolución de la vida en una dirección positiva y no negativa. Necesitamos un conjunto de leyes evolutivas, que son lo contrario de las leyes de diseño rígidas como la zonificación monofuncional. Además, esas leyes tienen que permitir la reconexión de las unidades urbanas para mantener o aumentar el grado de vida en el entorno.
Nuestra civilización es lo suficientemente inteligente como para lograr lo que quiere. El problema es que un segmento importante de la población actual quiere en realidad regiones urbanas muertas. La gente busca las mismas cosas — como una geometría monumental simplista, una zonificación monofuncional, prioridad para el tráfico de automóviles, bloques comerciales y residenciales vallados y obligar a todos los pobres a vivir en enormes bloques de apartamentos — que destruyen la vida de una ciudad. Los pobres han recogido las mismas imágenes, por lo que tras ascender en la sociedad se unen inevitablemente a otros ciudadanos de clase media para matar su ciudad. La legislación urbana crea el tipo de ciudad que tenemos hoy en día; una legislación radicalmente diferente podría volver a crear una ciudad viva, si se puede convencer a la gente de que sus vidas y las de sus hijos serían mejores.
Conclusión
Mi propósito en este artículo era presentar nuevos resultados teóricos sobre la estructura urbana que se derivan de la parcelación de sistemas complejos coherentes. Estos resultados alteran drásticamente nuestra concepción de la ciudad como una simple yuxtaposición de edificios, ordenadamente alineados. Una ciudad sólo cobra vida si su geometría permite un enorme número de conexiones cambiantes, lo que le permite evolucionar de forma similar a como lo hace un organismo. Las conexiones responsables de la “vida” de una ciudad definen por sí mismas descomposiciones alternativas de la forma de la ciudad. Surge una imagen clara, la de una ciudad cuya complejidad se basa en muchas más conexiones de corto alcance que de largo alcance. Las ciudades necesitan restablecer un gran número de acoplamientos entre los vecinos más cercanos, así como un número considerable de ellos a varias longitudes intermedias. Además, la característica central de una ciudad viva es que reajusta constantemente todos sus vínculos. Por lo tanto, cualquier esfuerzo de planificación debe ayudar a este proceso natural de reconexión, en lugar de obstaculizarlo.
Versión castellana del libro “Principles of Urban Structure” publicado por Techne Press, Amsterdam en 2005. Traducción del inglés hecha por María Fernanda Sánchez.
veredes, arquitectura y divulgación está colaborando con el autor para publicar los capítulos de su libro “Principles of Urban Structure” traducidos gratis en la red, para el beneficio de los estudiantes hispanohablantes en todo el mundo. El libro en versión inglesa está publicado en Holanda, los EEUU y Nepal.
Referencias
Albert, R., Jeong, H-W. and Barabási, A-L. (1999) “Diameter of the World-Wide Web”, Nature, Vol. 401 pp. 130.
Alexander, Christopher (1965) “A City is Not a Tree”, Architectural Forum, Vol. 122 No. 1, pp. 58-61 and No. 2, pp. 58-62. Reprinted in: John Thackara, Ed. (1988) Design After Modernism (London, Thames and Hudson), pp. 67-84. “La Ciudad no Es Un Árbol”, https://sistemasdeproyecto.files.wordpress.com/2012/10/alexander-c-una-ciudad-no-es-un-c3a1rbol.pdf
Alexander, Christopher (2001) The Phenomenon of Life: The Nature of Order, Book 1 (Berkeley, California, The Center for Environmental Structure).
Alexander, C., Ishikawa, S., Silverstein, M., Jacobson, M., Fiksdahl-King, I. and Angel, S. (1977) A Pattern Language (New York, Oxford University Press). Un Lenguaje de Patrones, (Barcelona: Editorial Gustavo Gili, 1980).
Alexander, C., Neis, H., Anninou, A. and King, I. (1987) A New Theory of Urban Design (New York, Oxford University Press).
Courtois, P.-J. (1985) “On Time and Space Decomposition of Complex Structures”, Communications of the ACM, Vol. 28 pp. 590-603.
Edelman, Gerald M. and Tononi, Giulio (2000) A Universe of Consciousness (New York, Basic Books).
Gehl, Jan (1987) Life Between Buildings (New York, Van Nostrand Reinhold). [reprinted by Arkitektens Forlag, Copenhagen, Denmark, Fax 45 33912770]
Hillier, Bill (1997) “Cities as Movement Economies”, in: Intelligent Environments. Edited by: P. Droege (Amsterdam, Elsevier) pp. 295-342. Appears as Chapter 4 of: Bill Hillier (1996) Space is the Machine (Cambridge, Cambridge University Press).
Hillier, Bill (1999) “The Hidden Geometry of Deformed Grids”, Environment and Planning B, Vol. 26 pp. 169-191.
Hillier, W. R. G. and Hanson, Julienne (1984) The Social Logic of Space (Cambridge, Cambridge University Press).
Jacobs, Jane (1961) The Death and Life of Great American Cities (New York, Vintage Books).
Mikiten, Terry M., Salingaros, Nikos A. and Yu, Hing-Sing (2000) “Pavements as Embodiments of Meaning for a Fractal Mind“, Nexus Network Journal, Vol. 2 pp. 63-74.
Salingaros, Nikos A. (1998) “Theory of the Urban Web”, Journal of Urban Design, Vol. 3 pp. 53-71. “Teoría de la Red Urbana”, https://veredes.es/blog/teoria-de-la-red-urbana-nikos-a-salingaros/
Salingaros, Nikos A. (1999) “Urban Space and its Information Field“, Journal of Urban Design, Vol. 4 pp. 29-49.
Salingaros, Nikos A. (2000a) “Complexity and Urban Coherence”, Journal of Urban Design, Vol. 5 pp. 291-316. “Complejidad y Coherencia Urbana”, Veredes, arquitectura y divulgación, Madrid, España.
Salingaros, Nikos A. (2000b) “The Structure of Pattern Languages“, Architectural Research Quarterly, Vol. 4 pp. 149-161. “La estructura de los Lenguajes de Patrones”, https://veredes.es/blog/la-estructura-de-los-lenguajes-de-patrones-nikos-a-salingaros/
Salingaros, Nikos A. and West, Bruce J. (1999) “A Universal Rule for the Distribution of Sizes“, Environment and Planning B: Planning and Design, Vol. 26 pp. 909-923.
Simon, Herbert A. (1962) “The Architecture of Complexity”, Proceedings of the American Philosophical Society, Vol. 106 pp. 467-482. [Reprinted in: Herbert A. Simon, “The Sciences of the Artificial”, M.I.T Press, Cambridge, Massachusetts, 1969, pp. 84-118]
Simon, Herbert A. and Ando, Albert (1961) “Aggregation of Variables in Dynamic Systems”, Econometrica, Vol. 29 pp. 111-138.
Watts, D. J. and Strogatz, S. H. (1998) “Collective Dynamics of ‘Small-World’ Networks”, Nature, Vol. 393 pp. 440-442.






