Observaciones sobre la composición de la ciudad | Nikos A. Salíngaros
Capítulo 6 del libro «Principios de la Estructura Urbana», 2005, de Nikos A. Salíngaros.
Acerca de este capítulo — por Arthur van Bilsen.
Este capítulo1 trata de las propiedades fractales que comparten tanto las ciudades como los fractales matemáticos, tratando de no llevar demasiado lejos la analogía entre fractales y ciudades (como en la figura 2 de este capítulo). Las ciudades raramente se beneficiaran de las simetrías rígidas y de las estructuras que se encuentran en los fractales matemáticos. La palabra “fractal” significa “roto” que se opone a “continuo”. Utilizar en el diseño líneas (y superficies) fractales puede ayudar a los urbanistas y diseñadores a alcanzar gran parte de sus objetivos. Por ejemplo, una frontera fractal facilita las interacciones humanas y puede ser permeada por vías peatonales (ver, por ejemplo las figuras 1-5 en el capítulo 4, Complejidad y Coherencia Urbana).
¿Cuales son las propiedades fractales? Un fractal matemático
1. tiene una estructura en todos sus niveles y
2. es auto-semejante
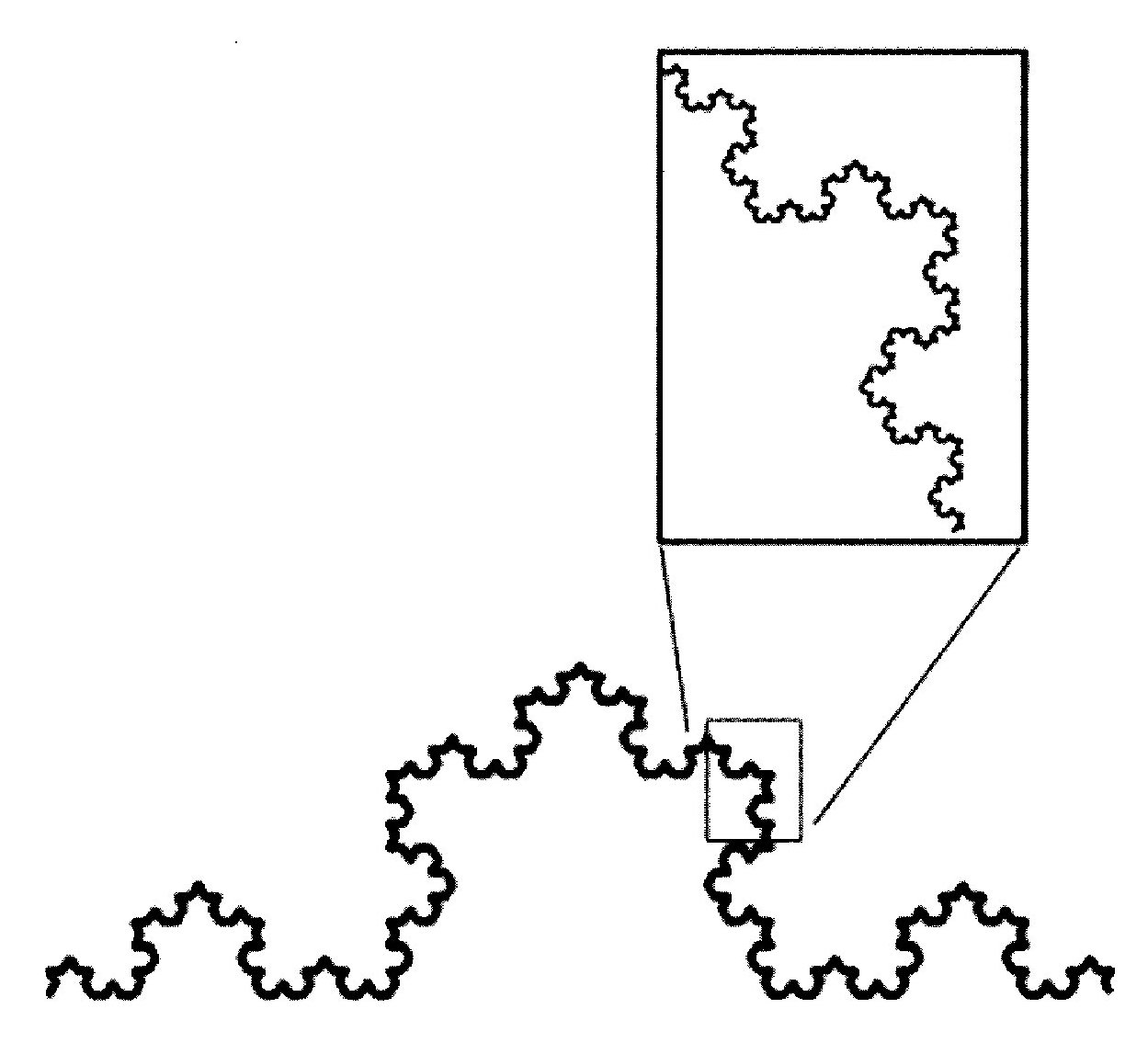
La primera propiedad (1) de un fractal es la existencia de una estructura en todas las escalas. Se encuentra esta propiedad en las ciudades, donde hay estructura en todas las escalas. La auto-semejanza (2) significa que partes de un fractal son similares a otras partes del fractal. Específicamente, se encuentran partes de la estructura repetidas en diferentes escalas (ver figura 1). La primera propiedad, especialmente, garantiza que se puedan usar elementos del concepto de fractal para mejorar la comprensión de la ciudad.
¿Cómo se puede construir un fractal? El fractal copo de nieve de von Koch, por ejemplo, puede ser construido poniendo un triángulo, sin uno de sus lados, en el tercio medio de un segmento de línea. Repitiendo este patrón un infinito número de veces para los cuatro lados que resultan, obtenemos una línea arrugada (ver figura II). Algunas de las propiedades de este fractal ya fueron calculadas en el Capítulo 3, en la Sección “El copo de nieve de von Koch”.
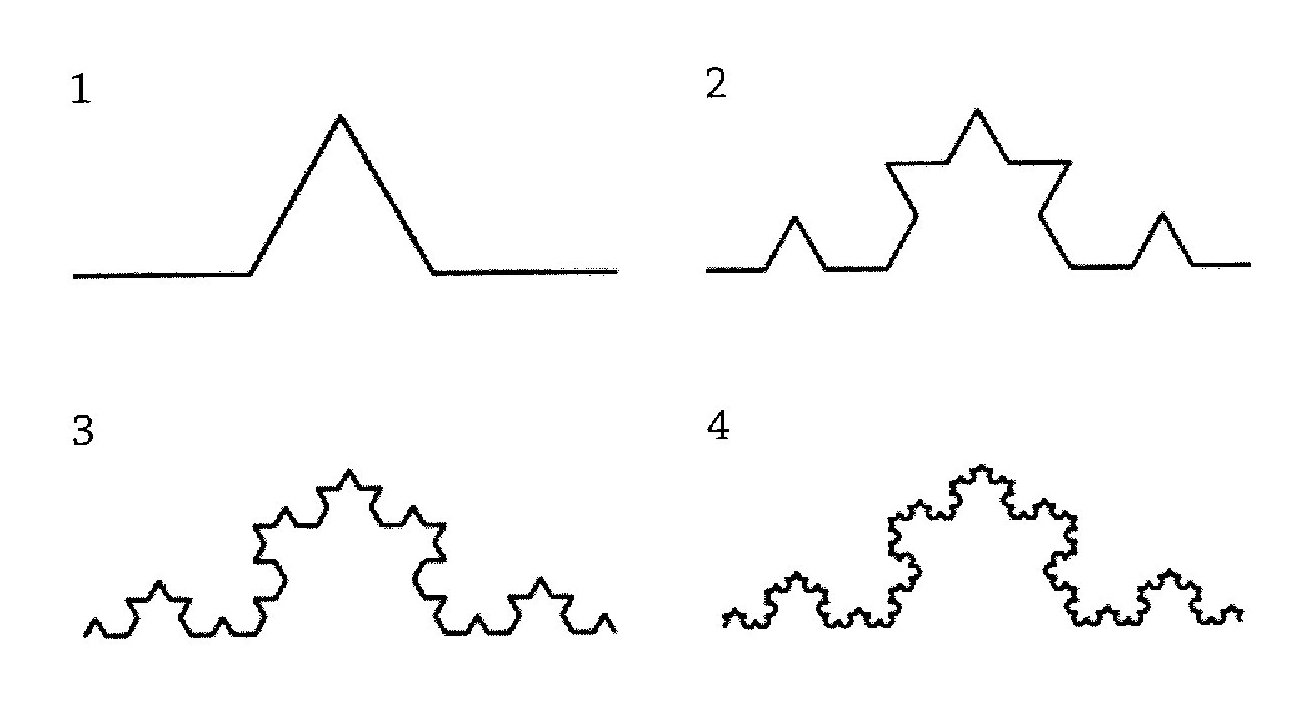
En realidad este proceso siempre se detendrá en una escala muy pequeña. Por ejemplo, el borde externo de una ciudad puede tener la longitud promedio de una fachada de un edificio como el elemento representativo de la escala más pequeña. El resultado también se adaptará a las influencias del entorno, que en algunas ocasiones ocasionan que su forma se desarrolle de manera asimétrica. Un buen ejemplo de fractal en el mundo real es la línea costera. La escala más pequeña en una línea costera depende de definiciones personales: por ejemplo, el instrumento de medición puede ser de 100 metros o de 10 metros o tan pequeño como un grano de arena 2 . Aunque un modelo es siempre una aproximación de la realidad, el hecho que un sencillo patrón pueda llevar a estructuras complejas y que también sea encontrado en la naturaleza (Mandelbrot, 1983) promete una mejor comprensión de estructuras complejas como las ciudades.
(NOTAS: Mandelbrot, B. B. 1983. The Fractal Geometry of Nature, New York: Freeman.
1 Discurso central presentado en la 5a Bienal de Ciudades y Urbanistas Europeos en Barcelona (Abril, 2003). Publicado en PLANUM — European Journal of Planning On-Line (Marzo, 2004).
2 Un hecho interesante es que la longitud de la costa no es fija, depende de la longitud del instrumento de medición utilizado. La longitud de la costa se incrementa en la misma medida que el instrumento de medición disminuye.)



Conectando la Ciudad Fractal
Las ciudades vivas tienen intrínsicamente propiedades fractales, una característica que comparten con todos los sistemas vivos. La presión por acomodar tanto el automóvil como el crecimiento de la población llevó a los urbanistas del siglo XX a imponer tipologías geométricas anti-fractales. Las propiedades fractales de la ciudad tradicional fueron eliminadas, con consecuencias desastrosas para el tejido urbano. Para deshacer este daño, es necesario entender muchas cosas con algún nivel de detalle: (i) cuales son esas propiedades fractales; (ii) la intrincada conectividad de un tejido urbano vivo; (iii) métodos de conectar y reparar el espacio urbano; (iv) una manera efectiva de sobreponer la red peatonal, los automóviles y los transportes públicos; y (v) como integrar conexiones físicas con conexiones electrónicas. Antes que nada, es necesario aclarar algunos malentendidos básicos acerca de la estructura fractal. Luego voy a subrayar la naturaleza e importancia de la coherencia jerárquica. Es posible utilizar el criterio fractal para poner a prueba la geometría de las ciudades como una condición para su éxito. Otro criterio independiente es la conectividad, que siempre ha de ser estudiada topológicamente. Para esto utilizaré las lecciones aprendidas a partir del estudio de la evolución de los sistemas biológicos y el internet para tratar el tema de la distribución de los tamaños, la Ley de Escalas en Potencia Inversa, y redes del tipo de “small-world” (mundo pequeño). Esos conceptos nos muestran como las densidades extremas favorecidas por el urbanismo contemporáneo — dispersión suburbana por un lado, y rascacielos en el otro — son patológicos. El reto para la ciudad contemporánea es como superponer de manera efectiva las redes que conectan y que compiten entre si.
Introducción
En este Capítulo se describen los diferentes tipos de ciudades caracterizadas por su geometría conectiva, y que tienen niveles de vida urbana muy diferentes. La vida de una ciudad depende directamente de su matriz de conexiones y su subestructura, ya que la geometría puede fortalecer o debilitar el movimiento e interacción de las personas. Esta comprensión es crucial para superponer la ciudad electrónica generada por las Tecnologías de Información y Comunicación. Contrario a lo que es ampliamente asumido, la ciudad electrónica no es un producto de la ciudad modernista “high-tech” ciudad del automóvil, pues en realidad se puede relacionar mucho mejor con la ciudad de escala humana del siglo XIX.
Con el fin de analizar esos aspectos puramente geométricos, es necesario tener una clara definición de los términos. Para esto dedico un tiempo en definir “fractal”, “scaling”, y “conectividad” en los Apéndices técnicos de este Capítulo. Los urbanistas podrían asumir, de manera incorrecta, el título de este Capítulo como “Conectar la ciudad desconectada”. Si, las ciudades contemporáneas están desconectadas, pero en un sentido distinto, pues ellas tampoco son fractales. La distribución de los tamaños de los componentes urbanos y sus conexiones pueden definir claramente diferentes tipos de ciudades. Una imagen emerge de una ciudad que se compone de diversas redes que interactúan, donde cada una de ellas funciona a diferentes escalas. A pesar que son redes que compiten entre si, esas mismas redes con especificaciones muy diferentes tienen que conectarse y cooperar perfectamente entre si, para poder definir una ciudad viva.
Pensar la ciudad como una estructura multi-fractal ha representado un gran avance conceptual (Batty & Longley, 1994; Frankhauser, 1994). Como urbanistas, nos hemos liberado de la engañosa idea de “una escala específica que define la ciudad”, ya que un fractal existe en todas las escalas. Diversos procesos y mecanismos urbanos que aparecen en diferentes escalas. La idea de acontecimientos que ocurren simultáneamente en todas las escalas y que al mismo tiempo cooperan de manera intrínseca, facilita entender como una ciudad vive y crece, y hace de la planificación un asunto mucho menos riesgoso. Este Capítulo muestra por qué las ciudades históricas son fractales mientras que las ciudades del siglo XX no lo son. La ciudad del futuro tiene que de nuevo convertirse en una ciudad fractal. Esto se logrará adaptando las soluciones geométricas más relevantes de las ciudades tradicionales, mientras que al mismo tiempo incorporando nuevas y apropiadas estructuras fractales para las nuevas exigencias y las nuevas tecnologías.
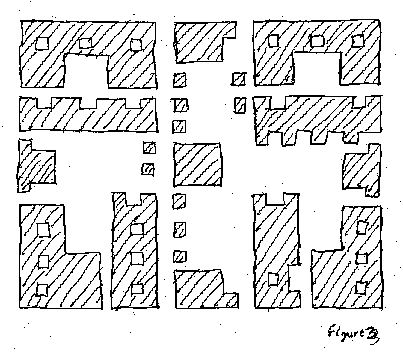
Este Capítulo inicia en describiendo que tipo de ciudad es fractal, y cual no. La idea central es la existencia de una estructura vinculante en todas las escalas de una jerarquía, desde las más grandes a las más pequeñas. Para los aspectos más técnicos, conviene leer el Apéndice I. Después, bosquejo la conectividad que hace que una ciudad sea viva. Las ciudades vivas tienen un número de conexiones entre nodos muy superior que las que se deberían esperar de una ciudad modernista. Para que esas conexiones se desarrollen de manera natural, requieren de una enorme variedad de nodos unos junto a otros en una estrecha interrelación. Por tal motivo, la zonificación monofuncional — la idea central de la planificación urbana del CIAM — impide la vida en una ciudad (Figura 1).
El resto del Capítulo analiza la jerarquía de conexiones necesarias para mantener la vida urbana. Las redes que compiten entre si existen en muchas escalas, siendo necesaria cada escala para funciones separadas. Entender esas interconexiones es esencial si deseamos incorporar la ciudad electrónica en la ciudad real. Cuestiono la política de eliminar las conexiones de pequeña escala a favor de las conexiones de gran escala — la ciudad necesita de las dos, y en el equilibrio justo. Las ciudades de hoy tienen una interfaz completamente inadecuada entre el espacio de los peatones y de los automóviles, y al respecto retomo las propuestas hechas por Christopher Alexander que dan una solución a este problema. Posteriormente, analizo la eficiencia de las redes, introduciendo la idea de las redes de tipo “small-world”.
Existe un gran vacío en el pensamiento sobre lo urbano — la falta de un marco epistemológico en el cual se pueda verificar si en realidad las actuaciones sobre la ciudad generaran el efecto deseado, o si ellas, por el contrario, degradan el tejido urbano. Determinar la causalidad de las actuaciones sobre lo urbano (i.e., qué causa qué) es esencial antes de actuar. Hago un llamado por un acercamiento más inteligente y científico de las intervenciones urbanas. El Capítulo concluye con sugerencias sobre como regenerar el tejido urbano. Mis propuestas incluyen ideas de Christopher Alexander y Léon Krier para restablecer la red peatonal, guiados por nuestros recientes avances en el conocimiento de la estructura del World-Wide Web.
Tres Apéndices técnicos describen con más detalle las matemáticas de la forma urbana. Primero hablo sobre fractales y el concepto de scaling, mostrando como un fractal es en realidad una sofisticada estructura conectiva entre todas las escalas. Segundo, comento la distribución de los tamaños, lo cual nos dice cuantas partes de determinado tamaño existen si siguen una escala fractal. Este resultado se aplica al tamaño de los barrios, edificios, espacios urbanos, espacios verdes, calles y caminos. Tercero, hablo sobre que tipo de distribución física de acuerdo a los tamaños es compatible con las conexiones electrónicas. Desde un punto de vista matemático, la ciudad electrónica se relaciona mejor con una ciudad tradicional que tenga conexiones peatonales, y este resultado es corroborado por los patrones evolutivos de las interfaces espaciales/electrónicas.
¿Qué tipo de ciudad es fractal?
Únicamente las antiguas y pre-modernistas ciudades son fractales, porque ellas funcionan en todas las escalas. Las ciudades medievales son las más fractales desde las escalas más pequeñas, hasta la escala superior de 1 Km., mientras que las ciudades del siglo XIX funcionan mejor en escalas mayores. Las tipologías urbanas usadas a lo largo de la historia hasta el siglo XX condujeron automáticamente a una estructura fractal (Salingaros, 2001) (ver figuras 2 y 3). La forma urbana tradicional sigue la red peatonal de transporte. La ciudad predominantemente peatonal fue construida a lo largo del tiempo — con continuas, y cada vez mayores, adiciones — basándose en un modelo fractal, sin que sus constructores fueran conscientes de ello. Como lo he propuesto en otros lugares, la mente humana tiene un modelo fractal impreso, que hace que lo que genera intuitivamente tenga una estructura fractal (Mikiten, Salingaros y Yu, 2000).
La gente actualmente tiene que estar sicológicamente condicionada antes de poder crear objetos no fractales. Desafortunadamente, esto es justo lo que nuestra educación y medios de comunicación han estado haciendo desde hace muchas décadas. La “imagen de modernidad” es de líneas elegantes, bordes geométricos abruptos, y es probable que esta sea la fuerza más poderosa que moldea nuestras ciudades. No importa que esto no tenga nada que ver con el como una ciudad funciona — la idea más simple es la que nos empuja a construir. Aún más alarmante, es que esta fuerza también decide que partes del tejido urbano existente se van a destruir por “no estar de máxima actualidad”. Hemos adoptado una colección de criterios de actuación irrelevantes para la vida urbana y destructivos con el tejido urbano.
La ciudad ideal de Le Corbusier es una concepción puramente de gran escala, y por lo tanto no fractal. Sus componentes son rascacielos, autopistas, y grandes espacios abiertos pavimentados. Le Corbusier dibujó rascacielos situados en parques gigantes, todo había sido definido tan solo en las dos o tres escales más grandes. Existen pocas estructuras claramente definidas en el infinito rango de escalas menores al ancho de los rascacielos, y en realidad no hay nada a la escala humana que va desde 1 cm. hasta 2 m. Él perdió de vista la necesidad de las escalas más pequeñas en una ciudad viva. Le Corbusier malinterpreto totalmente como debería parecer la “ciudad del futuro”. Sus rascacielos, por lo tanto, reemplazaron el tejido urbano vivo de las ciudades tradicionales, pero no se situaron en los parques gigantes — las fuerzas urbanas decretaron que deben situarse en aparcamientos gigantescos.
Por otro lado, la intervención realizada por Haussmann en Paris puede ser explicada por un proceso de scaling fractal. Cuando la Paris Medieval había crecido más allá de un cierto tamaño, en el cual sus estrechas calles no podían seguir soportando el tráfico, fue necesario añadir estructuras de una nueva y mayor escala. Por lo tanto, era necesario destruir parte del tejido urbano con el fin de ampliar el ancho y la longitud de algunas calles. El Papa Sixto V hizo lo mismo en Roma. El mismo proceso estaba detrás de la introducción de grandes parques urbanos — una vez que la ciudad se extiende más allá de determinada área geográfica, se crea la necesidad de áreas verdes más grandes. Ejemplos de grandes parques construidos en el siglo XIX que reemplazaron el tejido urbano pueden ser encontrados en todas las grandes ciudades. En el siglo XX, sin embargo, esas intervenciones urbanas de gran escala (calles y parques) fueron malentendidas, y tan solo su aspecto destructivo fue copiado como modelo.
La morfología urbana es un producto específico del sistema de transporte establecido por los gobernantes cuando la ciudad fue fundada. Modificaciones posteriores al sistema de transporte lleva a cambios en la estructura de la ciudad. Hoy en día, los gobiernos legislan exclusivamente un modelo basado en la ciudad del automóvil (al legislar primero la red de carreteras y su infraestructura antes que cualquier otra cosa), o destruyendo la ciudad del peatón con el fin de convertirla en una ciudad del automóvil. En la segunda fase, los trozos de la antigua ciudad del peatón pueden sobrevivir como un recuerdo de la vida urbana (si el estado es verdaderamente eficiente, no quedará nada). Por esta razón, es extremadamente difícil transformar una ciudad del automóvil de la post-guerra o un suburbio en una ciudad del peatón — tenemos que construir una nueva red peatonal en la ciudad del automóvil.
La arquitectura contemporánea — incluyendo esos estilos que reaccionan frente al modernismo mínimo — sigue siendo anti-fractal. La razón es que rechaza la complejidad organizada en las escalas humanas que van desde 1 cm. hasta 2 m. Los edificios Postmodernistas y los Deconstructivistas, con muy pocas excepciones, han heredado la prohibición de los patrones, el diseño, el ornamento, y los materiales y superficies decorados. Su vocabulario consiste en materiales high-tech y superficies “puras”, y su lenguaje estructural es incoherente. En cuanto se pierda la jerarquía estructural y conectiva de las escalas pequeñas, la ciudad deja de ser fractal. A pesar de los engañosos llamados de sus defensores, la desorganización intencionada que caracteriza el estilo arquitectónico deconstructivista se opone a la organización interna de un verdadero fractal.
Conectividad y la trama urbana
La vida de una ciudad viene de su conectividad (Dupuy, 1991). Todo lo que hace la geometría es facilitar el soporte a una red conectiva de tal manera que las interacciones humanas puedan darse. Esa es la primera razón por la cual la gente escoge vivir en las ciudades. Necesitamos analizar las propiedades conectivas de los gráficos aleatorios para tener una mejor idea sobre como surge la vida en la ciudad (ver Capítulo 1, Teoría de la Red Urbana). Primero consideremos como se forman las conexiones. Cada conexión se da con el fin de realizar un intercambio de información entre dos nodos (Castells, 1989; Meier, 1962). Esta información puede ser codificada como bienes tangibles. Por ejemplo, una persona necesita ir desde su casa hasta su oficina. Los dos nodos son “casa” y “oficina”, y se deben conectar. Una estructura de caminos físicos debe facilitar esta interacción, de otra manera la persona no puede funcionar.
Los nodos se conectaran por medio de caminos en una manera absolutamente abstracta. Supongamos que comenzamos sin ninguna conexión, y luego conectamos un par de nodos, un par diferente cada vez. No tratamos de conectar de manera deliberada todos ellos — cada conexión se establece de manera aleatoria, e incluso entre dos nodos que ya están conectados con otros. Un resultado matemáticamente importante, gracias a Erdös y Rényi, es que después de un número determinado de iteraciones, la mayoría (es decir, más del 80%) de los nodos se conectarán de manera súbita (Barabási, 2002). Esto se debe a la formación de muchas redes de nodos que están conectados, que irán creciendo en número en cada iteración. En el umbral establecido por Erdös y Rényi, las redes independientes se conectarán entre si y formarán una gigantesca red, y por lo tanto vinculando la mayoría de los nodos (Figura 4).
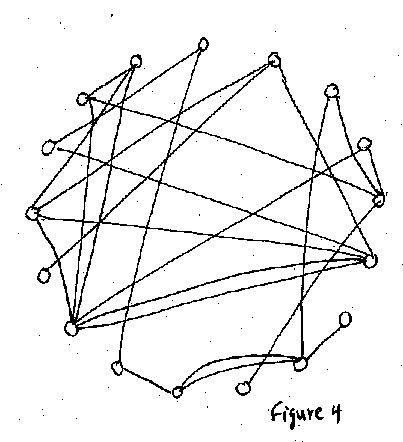
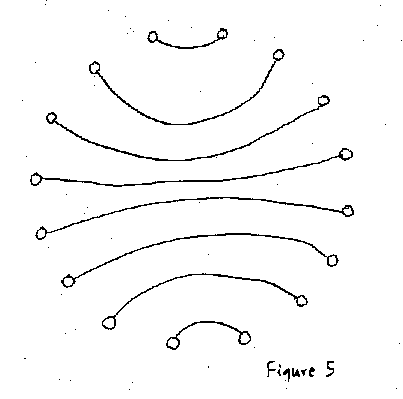
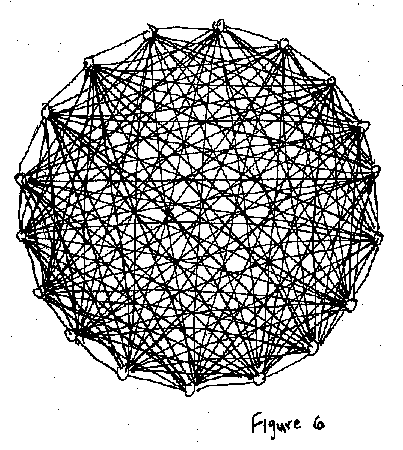
El número relativo de conexiones establece como funciona una ciudad viva (Alexander, 1965). Conectar de manera intencional N nodos de la manera más simple de tal manera que dos nodos están conectados en parejas por medio de un enlace requiere de (1⁄2)N caminos (Figura 5). Es decir, la mitad de los nodos son casas, y la otra mitad son oficinas, y cada casa está conectada a una oficina. Esta red está aún menos conectada que un gráfico de tipo “árbol” (Alexander, 1965). El número de caminos necesarios para alcanzar una conectividad aleatoria es aún mucho mayor (1⁄2)N ln(N). Con este número de caminos, la mayoría de nodos están conectados aunque sea por nodos intermedios (Figura 4). Avanzando un poco más, la conectividad completa — en la cual cada nodo está conectado DIRECTAMENTE con todos los nodos sin nodos intermedios — requiere de (1⁄2)N2 caminos (para un gran número de nodos) (Figura 6).
Aplicar esos resultados a una ciudad proporciona los rangos superiores e inferiores del número mínimo de caminos. La vida urbana es la interacción hecha posible cuando los nodos en una ciudad están conectados entre si, ya sea directa o indirectamente. Es de esperar, por lo tanto, que una ciudad viva con N nodos tenga un número de caminos que esté entre (1⁄2)N ln(N) y (1⁄2)N2 . Para que la red de transporte de la ciudad tenga todas esas conexiones, la red debe tener muchas capas. Además, la infraestructura debería ser lo suficientemente detallada para permitir una gran cantidad de alternativas y elecciones, lo cual genera, por permutación, un número mayor de caminos alternativos. Esto es lo opuesto a la consolidación de un gran número de calles y pequeñas manzanas en medio de superautopistas y supermanzanas de las ciudades de la post-guerra, un proceso que reduce de manera significativa el número disponible de caminos.
Para una ciudad, N puede igualarse al número de habitantes. Asumiendo N = 200,000 obtenemos los siguientes estimativos del número relativo de caminos conectivos. Una ciudad modernista de este tamaño tiene 105 caminos, mientras que una ciudad aleatoriamente conectada tiene 1.2 x 106 caminos, o lo que es lo mismo 12 veces que los que se encuentran en la ciudad modernista. Además, una ciudad completamente conectada tiene 2 x 1010 caminos, o 200,000 veces que las de una ciudad modernista. La ciudad medieval estaba conectada en su totalidad por medio de caminos peatonales. Nosotros construimos ese tipo de ciudades precisamente para permitir conexiones directas entre todos los nodos, y nuestra memoria colectiva no ha olvidado la libertad personal de movimiento e interacción que esto nos daba.
Nuestro deseo por conexiones directas por medio del automóvil entre cada uno de los nodos urbanos, hizo que la ciudad del automóvil se diferenciara de la ciudad modernista. La ciudad del siglo XX es la combinación de una ciudad del automóvil suburbana y una ciudad modernista. En teoría, podemos conectarnos utilizando el automóvil con cualquier otro punto, siempre y cuando exista aparcamiento, y que ningún otro automóvil quiera usar la red en el mismo momento. El automóvil incrementa el alcance de una persona en decenas de kilómetros. Aún más importante es el transporte y entrega de bienes por medio de camiones. El precio de la accesibilidad del automóvil, es sacrificar el 50% de la superficie de la ciudad para calles y aparcamientos, y hacer de nuestras economías rehenes de las provisiones de petróleo. Le Corbusier quiso fusionar los caminos de una ciudad modernista (105 en nuestro ejemplo) en un único supercamino (ver Capítulo 1, Teoría de la Red Urbana). Su método fue el de poner todas las viviendas en unos cuantos edificios gigantescos de gran altura, y todas las oficinas juntas en los rascacielos del centro de la ciudad.
Complementariedad y catálisis
Un principio fundamental es que las conexiones tan solo se pueden formar entre nodos complementarios. No existe ninguna razón para que nodos similares — con características funcionales similares — se conecten (Capítulo 1, Teoría de la Red Urbana). Muy poco intercambio de información puede ser posible entre nodos del mismo tipo. Las fuerzas que permiten que la ciudad funcione son generadas por la diversidad y la necesidad de intercambio de información entre nodos de diferentes tipos. Por consiguiente, no tiene ningún sentido, desde el punto de vista de la conectividad, agrupar físicamente nodos del mismo tipo en un área geográfica. La zonificación homogénea de nodos en regiones monofuncionales obliga a que nodos que no interactúan entre si, estén en una proximidad geométrica por razones tales como el beneficio de algún promotor, o el deseo superficial de un orden visual simplista. Esa es la antítesis de las normas básicas de las interacciones.
Las regiones homogéneas que violan el anterior criterio de complementariedad no deben ser confundidas con la coherencia alcanzada por los barrios con identidad propia. Un barrio es una parte de la ciudad que contiene la suficiente variedad y funciones para convertirse parcialmente en autosuficiente — al menos al mismo nivel que ocupa en una región geográfica determinada. Podría tener un carácter social o étnico que lo hace particular. La coherencia que resulta cuando todos los nodos están conectados es una propiedad que caracteriza un tejido urbano saludable, que sostiene, y a su vez es sostenido por la cohesión social. Esto es lo opuesto a lo que ocurre cuando se obliga a personas y funciones a ubicarse en una región ya sea por una planificación insensata, o por la economía, como lo puede ser una ciudad dormitorio (de suburbio) sin nodos comerciales, un degradado conjunto de grandes edificios de apartamentos sin ningún almacén en su cercanía, o un rascacielos de oficinas sin viviendas en las inmediaciones.
Lo anterior nos conduce a la catálisis. Muchas reacciones químicas requieren de algún tipo de catalizador, pues de lo contrario el ritmo de la reacción es demasiado lento para ser eficiente. Stuart Kauffman (1995) estudió un modelo en el cual un conjunto de nodos lograba una catálisis mutua que le permitía convertirse en un conjunto autocatalítico. Cada molécula también tenía el papel de actuar como catalizador de las reacciones entre otros nodos. Los catalizadores se encuentran en las mismas moléculas que interactúan — no existe la necesidad de adicionar catalizadores si existe una variedad suficiente de moléculas. Kauffman encontró que existe una cantidad mínima de moléculas de diferente tipo que pueden ser agrupadas para que puedan ser definidas como un conjunto autocatalítico (el cálculo es el mismo que para el teorema de Ërdos-Rényi). Aplicado al urbanismo, esto implica que una ciudad para estar viva requiere de una gran diversidad de nodos en cercana interacción (ver Capítulo 5, Observaciones Sobre la Composición de las Ciudades). Cada trozo del tejido urbano cataliza las interacciones entre los otros trozos (Figura 7).
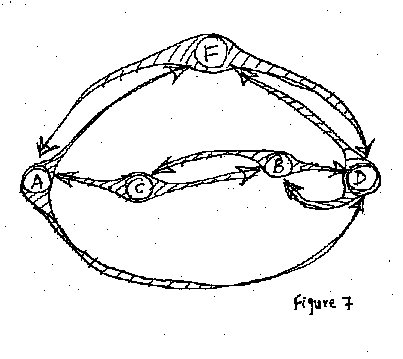
Esos resultados se refieren a un tejido urbano que está multi-conectado que funciona por autocatálisis. Brevemente esbozare dos de las implicaciones que esto tiene para la red urbana. Primero, a cada nodo se le tiene que dar una gran cantidad de caminos alternativos para conectarse con otros nodos. Por ejemplo, una persona debería tener las opciones de caminar, ir en bicicleta, conducir un automóvil, o tomar un bus público o privado (de servicios especiales), tomar el metro, el tranvía, o conectarse electrónicamente con otro nodo. A excepción del último, todos requieren de una conectividad lineal física, y por lo tanto competir por espacio entre si y también con las colocaciones físicas de los nodos. Esta cualidad impone una geometría fluida en la ciudad, la cual es radicalmente diferente de la geometría visual cúbica y desconectada que caracteriza el paradigma actual de la arquitectura y del urbanismo.
Segundo, debemos tener la suficiente densidad y variedad de nodos de tal manera que ellos catalicen sus propias interacciones. La vibrante ciudad del siglo XIX mezclaba edificios que contenían nodos dedicados a la vivienda, comercio, industria ligera, instituciones gubernamentales, y religiosas en una íntima interacción entre ellos (Alexander, Ishikawa, Silverstein, Jacobson, Fiksdahl-King, y Angel, 1977; Krier, 1998). La estructura física de la ciudad incluía los ahora perdidos referentes urbanos como los andenes, los bulevares, y el mobiliario de las calles. Un restaurante cataliza los caminos entre las viviendas, mientras que a su vez las viviendas catalizan la circulación frente al restaurante. Todo esto ha sido destruido al fragmentar los caminos que conectaban nodos diferentes (levantando cercos y barreras), y concentrando nodos similares en áreas homogéneas. Ahora le damos prioridad a las necesidades de aparcamiento de la ciudad del automóvil construyendo grupos de nodos similares, pero desconectados.
Jerarquía de conexiones
El internet ofrece al urbanismo nuevas e interesantes posibilidades (Castells, 1989; Drewe, 1999; 2000; Graham y Marvin, 1996; 2001). Reemplaza muchas conexiones “sucias” que requerían una enorme cantidad de combustible e infraestructura. Mientras que el sueño de muchos tecno-urbanistas de sustituir el transporte físico por el teletrabajo no parece que fuera a ocurrir, la red electrónica ha comenzado a fusionarse con las redes tradicionales de transporte. Aquí nos encontramos con la paradoja de la ciudad contemporánea — hacemos todo lo que podamos para conectarnos virtualmente y por automóvil, pero estamos desconectados físicamente en la escala peatonal (Dupuy, 1991; 1995). No obstante, en la medida que reemplazamos las largas y agotadoras jornadas en automóvil por las conexiones electrónicas, más valiosa se vuelve la ciudad del peatón, aunque la hayamos perdido en muchas partes del mundo.
Muchos problemas del urbanismo están relacionados con la escala. Una ciudad necesita estar conectada en todas las escalas. El tipo de conexiones que funcionan a diferentes escalas son muy diferentes entre si (Figura 8). Además, como las conexiones orientadas son más económicas en una superficie plana (a nivel del suelo), esto significa que conexiones de diferente tipo van a competir entre si (Dupuy, 1991; 1995). Una ciudad tiene que equilibrar todas esas conexiones. Como en cualquier otro problema de rivalidad, las conexiones más grandes/más fuertes son las que tienen la ventaja, y de forma natural desplazaran a las conexiones más pequeñas/más débiles. Existen razones fisiológicas y sicológicas básicas por las cuales los peatones requieren de las conexiones de pequeña escala a nivel del suelo. A no ser que estén protegidos, esos caminos están en riesgo por otras redes más fuertes.
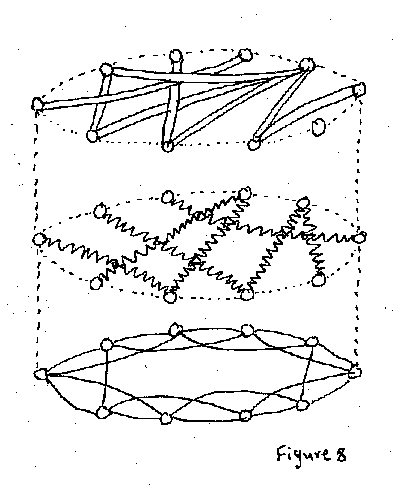
Tenemos que tener presente que las conexiones de gran escala se establecen estrictamente de acuerdo a su lugar en la jerarquía. Entender este proceso de manera equivocada lleva a que sutilmente fuerzas relacionadas con el transporte inciten a la construcción de más superautopistas, mientras que son eliminadas las escalas inferiores de la jerarquía (Dupuy, 1995). La red de transporte — en especial para los camiones pequeños — depende en la actualidad de la conectividad y no en la velocidad. Mucho más pequeñas, las angostas calles son necesitadas para conectar el tejido urbano — y en muchos casos, es necesario reintroducirlas como woonerven (calles angostas semi- peatonales cuya superficie limita la velocidad de los vehículos). La totalidad de la ciudad del peatón puede ser de nuevo construida como una red resguardada y entrelazada con el mar que forma el tráfico de automóviles (Krier, 1998).
En la mayoría de ciudades contemporáneas, la red de transporte borra los niveles inferiores en un insensato esfuerzo para convertirse en más “eficientes”. La gente pide acceso instantáneo a vías expresas, con casas y comercios junto a ellas. Ellos quieren saltarse la jerarquía de conexiones que estén por debajo de la escala más grande. Demasiadas autopistas están siendo construidas hoy en día, y demasiadas carreteras de media-baja capacidad están siendo ensanchadas. Por supuesto, la ciudad y el número de automóviles están creciendo, y pronto excederán cualquier nueva capacidad provisional de la red. No tiene sentido el estar constantemente actualizando toda la red de transporte vehicular hacia las escalas mayores, porque esto destruye las escalas más pequeñas.
Capilaridad y estructura fractal
Mi propósito con este Capítulo es aclarar los mecanismos por medio de los cuales la sociedad se conecta en los niveles del vecindario y de las calles. Creo que la estructura conectiva en esas escalas está esencialmente dañada. Tan solo después de haberla reparado podemos adaptar nuevos patrones a la extensión y accesibilidad de la red. Esto lo quiero analizar en términos de la difusión a través de canales capilares (Figura 9). El transporte no coordinado ocurre por medio de difusión. La difusión es un flujo no canalizado — es el movimiento aleatorio de partículas en la más pequeña escala. Esto se convierte en un flujo cuando todos los movimientos de menor escala son orientados hacia la misma dirección.
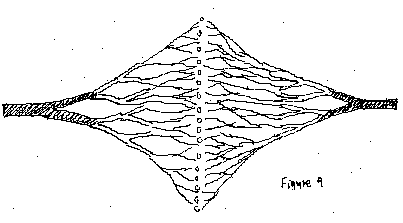
Con el fin de conectarse con otra red, los elementos que usan la primera red tienen que trasladarse a través de una interface a la segunda red. Donde exista flujo, este tiene que ser ralentizado cuando entra a los canales fractales (i.e., progresivamente más estrechos) que conducen hacia la interfase (Figura 9). En contraste, una red acelera su flujo al deshacer la estructura fractal canalizando el flujo. En el primer caso, las restricciones geométricas crean un nivel inferior como los vasos capilares en el sistema circulatorio humano, donde el flujo es más lento y difuso, aunque todavía es alimentado por el sistema circulatorio. La capilaridad es lo opuesto a un flujo rápido. En los niveles superiores de la red, los canales son amplios y uniformes para optimizar un flujo rápido. Una red saludable requiere de todos los niveles, desde los más rápidos hasta los más lentos.
Cuando no se comprende la estructura fractal de las redes urbanas, las ciudades tratan de maximizar su flujo en todos sus puntos, y durante el proceso eliminan su estructura capilar. La obsesión por las escalas más grandes en las redes del automóvil conduce a la geometría urbana desconectada que se observa en la actualidad. El error radica en no reconocer la estructura de múltiples redes relacionadas, que necesitan ser fractales con el fin de poder conectarse entre si. Para poder funcionar por si mismas, ellas también tienen que ser fractales, siguiendo las normas estructurales de los sistemas complejos (ver Capítulo 5, Observaciones Sobre la Composición de las Ciudades). En los inicios del siglo XX los urbanistas reconocieron la existencia de una gran cantidad de redes urbanas que competían entre si, pero en lugar de imaginarse sobre como acomodarlas, ellos decidieron deshacerse de aquellas que consideraban “anticuadas”.
La omisión más manifiesta en las ciudades contemporáneas es una interfase automóvil/peatón totalmente inadecuada. Dos redes de características totalmente diferentes pero que tienen que interrelacionarse perfectamente sin afectar la una a la otra. Christopher Alexander et al. (1977; Patrones 11, 22, 32, 52, 54, 55, 97, 100, 103, 113) señala la importancia fundamental de crear y mantener esta interfase fractal, y propone soluciones prácticas. Desafortunadamente, las ciudades en lugar de esto eligieron seguir las sugerencias opuestas del CIAM, ya que han trabajado de manera intensa en eliminar su red peatonal. El primer paso para destruir un sistema es eliminar sus puntos de acceso — i.e., su interconexión con otros sistemas. El encuentro entre los terrenos del peatón y del automóvil fue eliminado de tal manera que la ciudad del peatón pudo ser declarada entonces como “redundante”.
La interfase conectiva entre personas, espacios verdes, plazas y superficies construidas es tan importante como la interfase entre automóviles y personas. Nos conectamos de una manera más intensa en las escalas más intimas (Mikiten, Salingaros y Yu, 2000; en este libro Capítulo 2, Espacio Urbano y su Campo de Información). Esta es la razón por la cual amamos nuestros automóviles — tocamos su interior, que a su vez rodea nuestro cuerpo. Los espacios urbanos (con o sin zonas verdes) fueron hechos para envolvernos en un ambiente provocativo y confortable, pero recientemente los hemos hecho ajenos y hostiles. A menos una intimidad espacial nos conecte con las escalas más pequeñas, el espacio urbano es ineficaz. Siguiendo los dictados dados por una arquitectura modernista puritana, hemos despreciado la intimidad espacial en las ciudades de hoy en día por considerarlas como algo “no-moderno”, y la hemos eliminado.
Finalmente, necesitamos deducir los “patrones” en el sentido de Alexander et al. (1977) de la interfase que emerge entre la trama electrónica y la trama urbana. La llegada de la ciudad electrónica es tan revolucionaria como el crecimiento de la ciudad del automóvil (Castells, 1989; Drewe, 1999; 2000; Graham y Marvin, 1996; 2001). Una de sus consecuencias es la proliferación de los “café-internet” alrededor del mundo. Hay que resaltar que esta conexión se hace preferentemente por medio de la red peatonal. De hecho, la intimidad espacial sigue siendo valida para todos los puntos de acceso a la ciudad electrónica — el teléfono celular y el computador portátil se ajustan a nuestras manos. Esos diseños ergonómicos nos integran en la escala humana. A diferencia de la red de automóviles (pero más parecido al metro subterráneo), no vemos la trama electrónica debido a que esta no existe ni compite en ningún espacio físico.
Redes small-world y la World-Wide Web
Cuando he hablado de la conectividad me he referido hasta ahora, esencialmente a la topología de las conexiones. Para gran parte del análisis, no importa si los caminos son largos, cortos, rectos o curvos. A partir de la distribución de los tamaños sabemos, no obstante, sabemos que esos caminos satisfacen alguna distribución de acuerdo a su longitud, ancho, o capacidad (ver Apéndice II, al final de este Capítulo). Ahora es necesario analizar la longitud de estos enlaces con el fin de establecer una jerarquía de conexiones de acuerdo a su geometría.
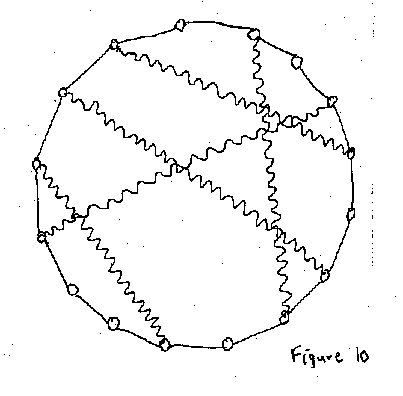
Una red small-world es donde los nodos están conectados por enlaces tanto largos como cortos (Barabási, 2002; en este libro en el Capítulo 5, Observaciones Sobre la Composición de las Ciudades). A partir de un conjunto de nodos que interactúan con tan solo sus nodos vecinos más cercanos, de manera aleatoria agregaremos unos cuantos enlaces de mayor longitud. El resultado es un drástico incremento de la conectividad general (Figura 10). Esto es medido por cuantos enlaces son necesarios para ir del nodo A al nodo B para cualquier par de nodos escogidos al azar. Si los nodos están conectados tan solo por medio de los nodos vecinos más cercanos, es necesario recorrer todos los nodos intermedios entre A y B. Con tan solo un par de conexiones más largas se generan atajos suficientes para mejorar la conectividad de la red. Lo que ha ocurrido es que un sistema compuesto tan solo por conexiones entre los nodos vecinos más cercanos (las más cortas) ha sido transformado en uno que es más cercano a tener una distribución de caminos que se ajustan a la Ley de Escalas en Potencia Inversa.
Este es el mismo resultado que se analiza en el Apéndice II, al final de este Capítulo. La diferencia es que ahora la red la hemos construido a partir de la escala más pequeña hacia la más grande. En la estructura urbana, esta progresión corresponde al crecimiento dinámico de un pueblo para convertirse en una ciudad, punto en el cual se pierde la conectividad inicial de pequeña escala. Para recobrarla, se necesita construir nuevas carreteras a manera de “atajos” para que conecten regiones espacialmente alejadas. Una red siempre tiende a ajustar su infraestructura de comunicación hacia una jerarquía que siga la Ley de Escalas en Potencia Inversa. Esta es la razón por la cual la ciudad medieval — con conexiones peatonales de corto alcance — no puede sobrevivir sin cambios.
Por la misma razón, no obstante, la ciudad modernista, que está artificialmente parcializada hacia las conexiones más largas, fue un modelo de planificación irreal. La ciudad del automóvil que emergió en lugar de la ciudad modernista, requiere de muchos trayectos cortos en automóvil, y por lo tanto aparcamientos en todas partes. Contrario a lo que Le Corbusier decretó, la gente nunca ha usado su automóvil para desplazarse tan solo entre su hogar en un suburbio ajardinado y su oficina del centro de la ciudad. Hoy el automóvil es usado para cualquier tarea de la vida cotidiana. Sin que sea sorprendente, una vez que logramos la sedentaria libertad de conexión que da el automóvil, exigimos una conexión directa para cada uno de los nodos urbanos. Esta poderosa fuerza crea los comercios suburbanos, eliminando el tejido urbano compacto existente.
La red de transporte urbano que conforma el metro, el tranvía, trenes ligeros y sistemas similares fue una invención de las ciudades que crecían rápidamente en el siglo XIX. Esto hizo necesario introducir atajos entre las partes de la ciudad del peatón que estaban demasiado alejadas para conectarse. La solución ideal era una red de transporte superpuesta que no compitiera con la peatonal y vehicular existente (de motor y tirado por caballos) y que fuera subterránea o elevada. El Metro debería ser interpretado como una extensión de la trama peatonal, ya que vincula partes de la ciudad que eran en si mismas partes de la trama peatonal. Todo esto en conjunto, es una red small-world que mejora su conectividad al introducir unas pocas conexiones de mayor longitud.
Entender esta causalidad (i.e., cual acción conduce a otra acción) de manera equivocada condujo a la desilusión cuando en la ciudad del automóvil se introdujo el metro. Tan solo por el hecho que París tenia metro, los suburbios post-guerra — con una cuadrícula de carreteras para automóviles ya construida — esperaban de manera poco realista que una porción del tejido urbano Europeo del siglo XIX se iba a desarrollar de manera milagrosa en torno a las estaciones de metro. Esto no se ha materializado. En una ciudad del automóvil, las fuerzas están abrumadoramente enfocadas a la necesidad de plazas de aparcamiento en torno a las estaciones de metro. Las fuerzas que podrían generan una red peatonal simplemente no están presentes, y las necesidades actuales pueden hacer que una trama peatonal nunca se forme allí.

La World-Wide Web ha crecido y esta auto-organizada de acuerdo a una auto- semejante estructura small-world (Barabási, 2002). Esto quiere decir, que obedece a la distribución de los tamaños que analizo en los Apéndices II y III, al final de este Capítulo, donde se analizan los enlaces conectivos (Figura 11). Ninguna de estas estructuras ha sido impuesta — todas han crecido de manera creciente. Aquí tenemos un excelente ejemplo de auto-organización, el proceso por el cual las fuerzas se ponen de acuerdo parar actuar de manera equilibrada y formar un sistema complejo dentro de una estructura funcional estable. Este proceso es análogo al milagro de crecimiento biológico de un embrión. Una combinación del código (dentro del ADN) y componentes químicos permiten la formación de una maravillosa estructura compleja.
Cuando las redes small-world fueron por primera vez presentadas, se descubrió que los sistemas nerviosos de los invertebrados (que son lo suficientemente simples para ser esquematizados) también cumplían esa distribución. La necesidad de tener una eficiente conectividad de las señales por medio del sistema nervioso ha hecho que los animales desarrollen el mismo tipo de redes. Una ciudad debería desarrollar el mismo tipo de conectividad, pero desafortunadamente no puede hacerlo de manera automática. Es necesario permitir tanto la auto-generación del tejido urbano en la pequeña escala, como intervenir deliberadamente en las escalas más grandes. De hecho este es uno de los problemas centrales del urbanismo — la competencia entre la imposición del diseño de arriba abajo, y un diseño auto-generado de bajo arriba. Los dos procesos están siendo malinterpretados en la actualidad.
El crecimiento de bajo arriba de las conexiones de pequeña escala permite la libre expresión de las fuerzas urbanas naturales. Sin embargo, si las conexiones se liberan de influencias externas y se les permite desarrollarse por si mismas, pronto surgirán estructuras aleatorias e incoherentes, como se observan en las favelas o los tugurios. La noción (y profesión) de “planificador” es una reacción al crecimiento incontrolado. Aún más, existe un enorme grado de vida que crece en tales condiciones. Bajo las condiciones adecuadas, las conexiones de pequeña escala pueden generarse más o menos de manera espontánea — todo lo que necesitamos es un poco de estímulo, orientación y algunas restricciones para garantizar una forma parcialmente coherente. Desafortunadamente hoy en día gran parte de las conexiones de arriba abajo destruyen las estructuras vivas. Las ciudades necesitan una planificación de arriba abajo, pero basada en como crece y se mantiene el tejido urbano.
Causalidad urbana
Debido al intercambio de información las fuerzas urbanas generan el tejido urbano, al igual que otras fuerzas urbanas pueden degradarlo o destruirlo. Una gran pregunta que no ha sido respondida es —
“¿Qué fuerza produce cual acción, o al contrario, cuales son las consecuencias de una intervención urbana en particular?”.
Difícilmente podemos esperar planificar de una manera realista a no ser que podamos anticiparnos a las consecuencias que tendrán las actuaciones e intervenciones urbanas. Tampoco podemos esperar entender como aparece la forma urbana si no captamos el carácter, la fuerza y la causalidad de las diferentes fuerzas urbanas. Esta parte de la pregunta todavía esta a la espera de ser sometida a una investigación intensa. Aquí tan solo puedo ofrecer algunas ideas preliminares.
A lo largo de este Capítulo, he tratado de mencionar casos de causalidad urbana que parecen lo suficientemente claros. Algunos de ellos son inesperados, y no obstante, van en contra de lo que es comúnmente aceptado. Mi aproximación a esos casos siempre ha sido científico — estudiar las actuaciones urbanas y sus consecuencias. Me temo que esto no es una práctica urbanística común. Uno podría disculparse, en parte, por esta omisión diciendo que es extremadamente difícil el aislar las intervenciones de sus consecuencias, debido a la complejidad del sistema urbano dinámico. Sin embargo, tenemos las herramientas científicas suficientes que nos permitan un primer acercamiento para desenredar la interacción de las fuerzas urbanas y establecer los mecanismos de la causalidad urbana.
Estoy particularmente preocupado por la frecuencia con que aparecen “virus” urbanos que no son reconocidos inmediatamente. Por esto me refiero a una idea, herramienta o práctica trivial que es presentada a la ciudad como inofensiva, pero que eventualmente la puede llegar a destruir. Un ejemplo histórico es el envenenamiento en Roma a causa del plomo con que eran construidas las tuberías, así como la costumbre de usar plomo en los vinos como conservante. Quizás en la actualidad estamos enfrentándonos patologías similares de las cuales no somos conscientes. Los gobiernos llevan a cabo escenarios de guerra imaginarios usando enormes simuladores informáticos (usualmente en simposios secretos), tratando de anticipar los peores desastres, e incluso las consecuencias de las más pequeñas acciones. Ellos están haciendo lo que es inteligente — planificando el futuro para que ellos no sean atrapados por sorpresa.
¿Por qué eliminamos la ciudad del peatón?
Queremos a la ciudad cuando podemos conectar con ella de manera íntima. Conservamos un recuerdo afectuoso de esa interacción. Este recuerdo está compuesto de conexiones visuales, olfativas, acústicas y táctiles. Todos esos recuerdos tan solo pueden ser formados en el nivel del peatón, a una escala mucho menor que la distancia más corta que pueda ser recorrida caminando. Nuestra inmensa memoria subconsciente de una ciudad está formada a un nivel visceral, a la escala de nuestros cuerpos. El “alma” de una ciudad existe precisamente en sus escalas arquitectónicas más pequeñas. Esto incluye el “detritus” que el modernismo trato de eliminar con tanto esfuerzo — paredes desalineadas y torcidas, un poco de color, pinturas raspadas, ornamentos arquitectónicos, una escalera, un árbol en la acera, un poco de pavimento, algo en lo cual apoyarse, un lugar donde sentarse, etc.
El movimiento anti-fractal del siglo XX comenzó con llamamiento a destruir el ornamento. El ornamento arquitectónico es una parte intrínseca de la ciudad en su conjunto, y destruyéndolo se destruye una parte de las escalas de la ciudad. Tal intervención elimina un nivel en la jerarquía urbana, las escalas que van desde 1 mm hasta 1 m. Poco después, los referentes urbanos — las estructuras que van desde 1 m hasta 3 m, como kioscos, bancos, pórticos, glorietas, paredes bajas para sentarse, etc. — fueron eliminadas. Por último vino la eliminación de los andenes y la conectividad vía peatonal entre edificios cercanos. Lo que quedó tan solo era apropiado para la ciudad del automóvil, no para el movimiento de los peatones. Es verdad, en los años 20 del siglo pasado era necesario acomodar al automóvil en la ciudad del siglo XIX, pero durante el proceso no era necesario destruir la ciudad del peatón.
Existen dos redes conectadas bien diferenciadas — la ciudad del automóvil, y la ciudad del peatón. Hemos permitido que la primera elimine la segunda. Esta intervención amputó los seres humanos de su entorno inmediato. Después de vivir de esa manera por muchas generaciones, los seres humanos han aceptado un estilo de vida desconectado, incluso aunque nunca puedan adaptarse ni física ni sicológicamente. Tristemente, es nuestra propia naturaleza biológica que nos hace aceptarlo de esta manera. Siendo esencialmente perezosos, preferimos sentarnos en un automóvil mientras que nos conectamos con nodos distantes a decenas de kilómetros — no existe necesidad de hacer intercambio entre diferentes modos de transporte. Sicológicamente, preferimos desplazarnos en la ciudad en nuestro propio (y personalizado) caparazón espacial, en lugar de mezclarnos con extraños en el transporte público. Queremos conectarnos a un almacén, una oficina, y a nuestro hogar directa y exclusivamente en automóvil.
La ciudad del peatón tiene algo importante que ofrecer y que compensa las ventajas de la ciudad del automóvil, en concreto — un ambiente físico rico en emociones. Hay un placer visual, la alegría del movimiento, la emocionante experiencia de una vida urbana vibrante, la estimulación sensorial de un espacio urbano lleno de personas de diferentes características y edades (experiencias que son esencialmente diferentes a las tensiones que producen el conducir por la ciudad). Le Corbusier desdeño todo esto, y sistemáticamente se ocupo de eliminarlo por completo por medio de las pautas de planificación del CIAM. Sus libros sobre urbanismo tan solo muestran los placeres de conducir en la ciudad en un automóvil deportivo. La eliminación del espacio urbano, los espacios verdes interconectados, y la escala humana del tejido urbano eliminó el único conjunto de fuerzas que generaban y mantenían la ciudad del peatón.
La vida urbana requiere una red de espacios urbanos peatonales interconectados, cuyos tamaños obedezcan la Ley de Escalas en Potencia Inversa (como se describe en el Apéndice II, al final de este Capítulo). La multiplicidad de caminos peatonales son albergados y protegidos por los espacios urbanos abiertos y semi-cerrados. Lo uno no puede existir sin lo otro. La red de espacios urbanos fomenta y coincide con los caminos peatonales (Krier, 1998; en este libro Capítulo 2, Espacio Urbano y su Campo de Información) (Figura 12). Los arquitectos ya no diseñan espacios urbanos donde la gente desee pasar el tiempo, de tal manera que los espacios urbanos construidos están totalmente desconectados de la red peatonal, y por lo tanto entre ellos. Este colapso en el concepto de la ciudad no es accidental — es la estricta aplicación de una geometría para el sistema de transporte que es incompatible con el espacio urbano, de la misma manera que el CIAM está predispuesto en contra del concepto mismo de espacio urbano (ver Capítulo 2, Espacio Urbano y su Campo de Información, y Capítulo 5, Observaciones Sobre la Composición de las Ciudades).
Los prejuicios modernistas frente a los automóviles y en contra de los peatones han mantenido el dogma nunca manifestado que
“los vehículos de motor no amenazan al peatón”,
un rechazo a una percepción sicológica fundamental. Por lo tanto, en lugar de diseñar un espacio urbano que proteja la gente de los automóviles tanto sicológica como físicamente, aún pretendemos que el espacio urbano no es necesario. La misma hipocresía le da prioridad a los automóviles siempre que el peatón y el automóvil se encuentren — lo opuesto a lo que debería ocurrir. Una regla básica de las ciudades vivas es que los peatones deben siempre sentirse seguros frente a los vehículos en movimiento.
Por un pequeño margen la anatomía humana ha frustrado el sueño de Le Corbusier de tener gente saludable entrando en sus automóviles en el garaje de sus hogares suburbanos, y saliendo en el aparcamiento de sus oficinas (mientras que la clase trabajadora se suponía que se las tendría que arreglar con el transporte público). Su visión de una ciudad sin una escala humana ha estado muy cerca de hacerse realidad. De todas maneras, aún en la ciudad más desconectada, anti-ciudad disfuncional, la gente camina diariamente desde y hacia su vehículo. Es imposible de eliminar totalmente el terreno del peatón. Como se supone que esos caminos peatonales cortos no existen, se dejan mal definidos. La alguna vez gloriosa ciudad del peatón se ha contraído a los garajes de concreto sombríos y los aparcamientos de asfalto baldíos.
Espacios verdes y geometría fractal
Las ideas de este Capítulo se aplican a los tamaños y la distribución de los espacios verdes. Una ciudad viva requiere una inmensa zona verde, muchas de tamaños intermedios, y una gran cantidad de tamaños pequeños. En una ciudad, deben de existir una gradación de los espacios verdes públicos que vayan desde los más grandes hasta los más pequeños parques para que los niños jueguen, situados muy cerca de sus casas. Esta propuesta es una verificación teórica de las ideas originalmente sugeridas por Christopher Alexander et al. en “A Pattern Language” (1977; patrones 51, 60, 67, 111 y 172). La práctica opuesta es la consolidación, siguiendo el mito de la “economía de escala”, que destruye la distribución natural de los espacios verdes. Los suburbios ofrecen lo que fue quitado de nuestras ciudades — un espacio verde para cada familia (pero tienen problemas con su conectividad y la baja densidad).
La conectividad sistémica ocurre (o no) independientemente de la distribución de los tamaños. Se puede ver esto en nuestras ciudades destruidas, si consideramos la distribución y la conectividad de sus espacios verdes. Se ha puesto de moda poner en lugares aislados trozos de verde ornamental (césped o arbustos) en muchos lugares inútiles. Aunque en principio es bueno tener esos espacios verdes, en realidad nadie puede caminar en ellos, puesto que están desconectados entre ellos y de los peatones. Sirven tan solo como decoración visual para la ciudad del automóvil, sin relacionarse de ninguna manera con la ciudad del peatón (que de hecho puede que sea inexistente). La presencia de espacios verdes de diferentes tamaños, incluso si siguen la Ley de Escalas en Potencia Inversa, no crean una red — primero deben conectarse en el rango de las escalas humanas.
Las ciudades del siglo XIX trabajaron muy duro para ofrecer una interfase conectiva entre el mundo natural de las plantas, los árboles y las rocas, y el entorno construido. Esto fue logrado por medio de la geometría. Hoy, todo lo que vemos es una geometría de aristas desconectadas. Una planta es una estructura intrínsicamente fractal, y en cualquier caso, no se ajusta a la geometría modernista de la máquina. El pensamiento anti-fractal es asombrosamente obvio sobre como el espacio construido está desconectado de las plantas. Una geometría no-natural ha sido impuesta en el mundo natural. El modernismo prefiere céspedes perfectamente lisos y arbustos cortados en forma de cubos perfectos. Sembrar un árbol en una maceta cuadrada es una yuxtaposición de dos geometrías excluyentes e irreconciliables.
Volviendo a la idea de conectividad, los espacios verdes fracasarán en su función urbana a no ser que podamos conectarlos físicamente a la escala del peatón. Céspedes y árboles inaccesibles, ya sea porque se encuentran en terrenos privados, o porque están al lado de una autopista, no forman parte del tejido urbano. Eso no es una reserva natural, que necesitan una protección de los peatones. Hemos sido confundidos por el pensamiento del CIAM que personifica la desconexión y segregación (no únicamente en relación con los espacios verdes, sino también con casi todo lo demás que tenga que ver con el tejido urbano).
Intervenciones para regenerar el tejido urbano
El obstáculo principal para la regeneración urbana es la filosofía de desconexión de nuestra sociedad. En la actualidad, tratar de introducir un tejido urbano vivo va en contra de la concepción de orden de la mayoría de personas. Nosotros adoptamos en el siglo XX una tipología urbana y arquitectónica de formas no-vivas, y este entorno construido ahora nos enseña un modelo no-vivo del universo. Nuestro entendimiento básico de cómo funciona el universo está influido por lo que nos rodea, acompañada por una filosofía que deshonestamente opone la modernidad a los procesos vivos tradicionales. Como resultado, la gente considera las formas urbanas y arquitectónicas sobrevivientes que expresan vida como “impuras”, “anticuadas”, e incluso “reaccionarias”. Desde este predominante punto de vista del mundo, es extremadamente difícil reconocer las estructuras vivas, lo cual es un pre-requisito para cualquier intervención enfocada a generar estructuras vivas.
Vuelvo a la regla básica que dice que la morfología urbana está determinada por la trama urbana de trasporte. Enfrentado con una ciudad disfuncional, la planificación innovadora no será efectiva a menos que la red de transportes y su infraestructura sean modificadas. Esto es muy difícil de lograr, y, además, es extremadamente costoso. Las ciudades podrían no querer comprometerse con una reorganización tan drástica también por razones filosóficas, ya que esto implica cambiar los códigos de crecimiento que corresponden a sus “genes”. Sin embargo, la mayoría de ciudades alrededor del mundo cambiaron exitosamente sus genes para renacer como una ciudad del automóvil a partir de la ciudad del peatón, por lo tanto, en principio es posible realizar el proceso contrario.
Hoy la regeneración urbana se diferencia en dos problemas principales — como revivir la ciudad del automóvil, y como revitalizar la ciudad del peatón degradada y muerta. En el primer caso, tenemos que construir una red peatonal al interior de la ciudad del automóvil, eliminando parte de esta en el proceso. Sorprendentemente, este objetivo puede ser alcanzado sin afectar de manera considerablemente la red de automóviles y camiones. No necesitamos sacrificar la conectividad. El segundo caso — las zonas degradadas (villas miserias, favelas) — son mucho más difíciles de solucionar, ya que están creadas por problemas sociales que expulsan la saludable mezcla de funciones urbanas que definen una ciudad viva. La gente que vive en los guetos está desconectada del resto de la ciudad por su elevado índice de criminalidad, drogas, y la falta de oportunidades de trabajo y educación. Ellos carecen de las conexiones sociales de gran escala para el intercambio de información.
No intento hablar de los problemas sociales que hacen más complicada la regeneración urbana de las zonas degradadas. Sin embargo, entender un aspecto de este complejo fenómeno es casi trivial. La gente con muy poco poder e influencia no debería ser culpada por los problemas urbanos de las zonas degradadas. Las clases económicas más poderosas sencillamente dejaron de considerar las zonas degradadas en el viejo centro como parte del medio ambiente urbano, y huyeron hacia los suburbios. Alguien tiene que llenar la parte que ha sido desalojada, y, como nadie con algún dinero lo considera como un lugar agradable para vivir, fue dejado para aquellos que no tenían otra alternativa. Bajo este punto de vista, los habitantes de las zonas degradadas cumplen una función urbana esencial, ocupar zonas que nadie más quiere.
Una combinación de métodos bottom-up y top-down trabajando conjuntamente pueden re-crear la ciudad del peatón protegida de la ciudad del automóvil, pero al mismo tiempo conectada a ella. El método top-down legislará la zonificación de uso mixto, y no promoverá concertaciones de funciones homogéneas. Las densidades mínimas y máximas serán ajustadas para escoger contra de los edificios altos, así como de los suburbios dormitorios de baja densidad. Por encima de una determinada densidad mínima (a partir de la cual son económicamente viables), podremos necesitar un porcentaje de nodos de negocios mezclados con las viviendas. Siguiendo la iniciativa del estadounidense Andrés Duany, miembro fundador del New Urbanism, es necesario cambiar los códigos, y entonces la ciudad evolucionará hacia una estructura viva. Los nuevos códigos establecerán que la mayoría de edificios son de uso mixto. Los edificios altos pueden permitirse en situaciones especiales, con la aceptación total que las densidades más altas son parasitarias de su entorno.
Otra posibilidad para la vida está en las fuerzas urbanas naturales. El componente bottom-up de la regeneración flexibiliza los códigos actuales para permitir la expansión por medio de la auto-construcción. Esto es un crecimiento aleatorio que produce los asentamientos ilegales y las ciudades periféricas del tercer mundo. Esto, no obstante, representa un auténtico proceso urbano vivo que no puede ser ignorado. Debería ser restringido de tal forma que no crezca fuera de control, ya que canalizar este proceso es mucho más inteligente que tratar de eliminarlo. Los planificadores han aprendido (pero rara vez lo admiten) que esta fuerza urbana NO PUEDE ser totalmente eliminada — el crecimiento incontrolado ocurrirá justo después del alcance de los organismos oficiales. Es mucho mejor enfocar esta fuerza creativa hacia la construcción de un tejido urbano que sea más útil, higiénico, y permanente.
La regeneración en áreas urbanas existentes, debería ser fomentada ofreciendo subsidios para el crecimiento en las escalas pequeñas. Este es el mejor y más eficaz medio para regenerar las escalas más pequeñas en las ciudades, que ahora están ausentes. En el presente, el gobierno subsidia principalmente los proyectos de gran escala, siguiendo una filosofía de planificación de intervenciones de gran escala. Es mucho más fácil gastar el dinero público en grandes cantidades — una lamentable contabilidad propia de todas las burocracias gubernamentales. Esta práctica tiene que ser modificada, de tal manera que los fondos sean divididos siguiendo a una Ley de Escalas en Potencia Inversa. Esto significa entregar un gran número de subsidios en una pequeña cantidad de dinero para proyectos pequeños — lo más pequeño, lo mejor (Alexander, Silverstein, Angel, Ishikawa, y Abrams, 1975; en este libro Capítulo 3, Una Regla Universal para la Distribución de Tamaños). Hoy en día la construcción de cosas pequeñas está casi universalmente desaconsejado, o incluso prohibido por las leyes de la zonificación.
Conclusión — La ciudad del futuro
Si podemos deshacernos de las vendas ideológicas impuestas en el mundo por las bien intencionadas pero falsas ideas acerca de la “modernidad”, entonces comenzaremos a entender como se forma y cambia dinámicamente el tejido urbano. Luego podremos construir nuevas ciudades que incorporen las mejores características de las ciudades tradicionales, mientras al mismo tiempo se utilizan las tecnologías de punta para facilitar, en lugar de frustrar, las interacciones humanas. Al mismo tiempo, podemos regenerar ciudades antiguas, que ya contienen estructuras que por sus costos hoy en día serían imposibles de duplicar. Esos edificios y espacios urbanos están siendo sacrificados por un intolerante dogma del diseño, para ser reemplazados por bloques rectangulares, cubos y aparcamientos sin fachada y sin vida.
Los componentes patológicos de la ciudad pueden ser descartados. Ya sea por una baja concentración o por una concentración excesiva de nodos las infraestructuras y los recursos de la ciudad son llevadas al límite. Dos extremos son la dispersión urbana, y los rascacielos. Los individuos desean la primera, mientras que los gobiernos y las empresas prefieren lo segundo. Ninguna de las dos posibilidades puede ser aceptada. La primera de esas tipologías usa la mayoría del combustible en las más simples necesidades de transporte. La segunda concentra en un edificio personas que no interactúan, sustrayendo recursos del resto de la ciudad. Las fuerzas urbanas producidas por la elevada concentración propia de los rascacielos, tienden a eliminar el tejido urbano en un área significativa alrededor del edificio. Los rascacielos se alimentan del resto de la ciudad, y requieren más infraestructura y vías expresas más grandes para mantenerlas.
La ciudad electrónica brinda ayuda en dos formas diferentes. Primero, reemplaza muchas conexiones “sucias” de la ciudad antigua, liberando infraestructura y consumo de combustible. Esto hace que los lugares peatonales de la ciudad sean mucho más atractivos y viables como nunca antes. Segundo, su estructura nos ofrece un modelo para continuar en la reconstrucción del tejido urbano. Hablé sobre como el Internet sigue las mismas leyes estructurales que la ciudad tradicional. Esto debería ser suficiente razón para descartar definitivamente los modelos insensatos y simplistas de urbanismo del siglo XX que han hecho tanto daño a nuestras ciudades. Si necesitamos conectar la ciudad electrónica con la ciudad física, entonces la ciudad física debe seguir las mismas leyes estructurales. Aplicando selectivamente prototipos exitosos del pasado, junto con aportes de la ciencia de las redes, podemos generar un modelo totalmente nuevo de ciudad contemporánea viva.
APÉNDICE I: FRACTALES Y SCALING
“Fractal” significa “roto”, aunque esto no es a lo que la palabra denota en matemáticas. Propiedades muy precisas caracterizan un fractal, las cuales usualmente no son entendidas por no-matemáticos. La idea esencial de un fractal es que tiene una estructura con una jerarquía de escalas. Una estructura definida por un tamaño promedio x significa que es parecido a un tamaño r x , donde r es un factor de escala como por ejemplo 1/3. Para que una estructura sea fractal, deben existir subestructuras a escalas decrecientes r2 x, r3 x , r4 x , etc. Un verdadero fractal matemático tiene estructuras auto-semejantes que van decreciendo hasta escalas infinitesimales. En un fractal físico, las escalas más pequeñas se vuelven imposibles de ver, y por lo tanto esto implica un rango de escalas que van desde las muy grandes hasta las muy pequeñas.
El número r es denominado “factor de escala”, y en teoría puede ser cualquier fracción. En la mayoría de fractales usualmente es un número fijo que está entre 1/2 y 1/10. Los fractales naturales (como las coliflores, las hojas de los helechos, y el pulmón del ser humano) tienen una estructura anidada con r no muy diferente que 1/3 (Salingaros, 1995; en este libro Capítulo 3, Una Regla Universal para la Distribución de Tamaños).
Existen dos formas de construir un fractal a medida que nos acercamos a las escalas más pequeñas. La primera es agregando una subestructura, mientras que la segunda es sustrayendo subestructuras. En el primer caso, al agregar una estructura en cada escala se crea un objeto doblado, arrugado, y con textura que en ninguna parte es llano o recto. Una “aspereza” fractal se genera en cada borde. Hemos creado la analogía de una superficie catalítica, donde los elementos químicos se encuentran para interactuar, atraídos por la superficie arrugada. En el urbanismo, los límites urbanos ondulantes facilitan las interacciones humanas, como por ejemplo el contorno de una plaza alineada con tiendas y mesas para tomar el café (Salingaros, 2001). Los espacios urbanos que son usados en la actualidad, están casi invariablemente rodeados por un límite fractal. El quitar la estructura fractal haciendo el borde más liso elimina la geometría catalítica propicia para la interacción peatonal, y destruye el espacio urbano (ver Capítulo 2, Espacio Urbano y su Campo de Información).
El otro método de construir un fractal es crear vacíos a escalas sucesivas y decrecientes, como si se estuviera troquelando un material. Los tamaños de los orificios se hacen más pequeños, formando un colador o una membrana perforada. En biología, las membranas tienen un papel tan importante como lo tienen las superficies catalíticas, ya que las membranas crean una interfase semi-permeable entre diferentes unidades biológicas. De la misma manera, las interfaces urbanas perforadas permiten a los peatones el circular a través de un límite urbano, al mismo tiempo que previene la circulación de automóviles por el mismo límite. Los ejemplos incluyen columnatas, pórticos, arcadas, entradas a pequeños comercios, bolardos a lo largo de un camino peatonal, etc. (Ver Capítulo 2, Espacio Urbano y su Campo de Información; y Salingaros, 2001). Los espacios entre los edificios son estructuras fractales a la escala de la ciudad. El aumentar el tamaño de las manzanas y construyendo paredes lisas sin entradas son intervenciones anti-fractales típicas de la planificación post-guerra.
Los fractales tienen otra propiedad muy importante — la coherencia y la auto- semejanza. Esto significa que las diferentes escalas están relacionadas por algún tipo de simetría de agrandar. En el más simple de los casos geométricos, un diseño es repetido en tamaños más y más pequeños, que sirven para ligar las diferentes escalas en un todo. En una aplicación mucho más sofisticada, en una ciudad viva los procesos y las estructuras a diferentes escalas cooperan de manera fundamental. Las estructuras coherentes de gran escala están compuestas de elementos de la escala pequeña. Esto es lo que unifica las diferentes escalas en un todo unificado y que interactúa tanto en términos de su geometría, como de los procesos dinámicos que ocurren en esas escalas.
APÉNDICE II: LOS FRACTALES Y LA DISTRIBUCIÓN DE LOS TAMAÑOS
¿Cuantos partes de la ciudad tienen un tamaño x ? Podrían ser copias del mismo tipo de objeto, o diferentes objetos del mismo tamaño. Asumiendo que una ciudad es fractal, entonces hay una respuesta sencilla — “existen p unidades de tamaño x , donde p es inversamente proporcional a x ”. Esto significa que entre más pequeños sean los componentes urbanos, más numerosos tienen que ser. Esta regla se llama exactamente “Ley de Escalas en Potencia Inversa”, y dice que p = C x–m , donde C y m son dos constantes que dependen de cada caso. Usualmente, m es un índice que está entre 1 y 2. (Para aquellos que quieran investigar esta formula, m es la dimensión fractal de Hausdorff). La otra constante, C , está relacionada con el mayor tamaño — en este caso la tamaño total de la ciudad (ver Capítulo 3, Una Regla Universal para la Distribución de Tamaños).
Mientras que la distribución de tamaños es una distribución continua (i.e., no existen restricciones de los tamaños posibles), en combinación con la regla de las escalas enunciada anteriormente, la distribución se vuelve discreta. Podemos denominar las escalas por un entero n , con un n que aumenta en la medida que se disminuya de escala, y hablar de la escala n-sima de la jerarquía. Ejemplifiquemos este concepto para un factor de escala r = 1/3 y una dimensión fractal m = 1.5. La distribución se convierte en pn = C (xn)–1.5 = 31.5n k , con k como constante. Por ejemplo, digamos que una ciudad sigue esta Ley de Escalas en Potencia Inversa. Existe una estructura — la ciudad — en la escala más grande. Fijemos, para el ejemplo, este tamaño total en 15 km. lo cual hace de la constante k igual a uno. Luego, existirán en la ciudad 5 estructuras bien definidas de aproximadamente 5 km de tamaño, aproximadamente 27 estructuras de 1.7 km., y alrededor de 140 estructuras de 556 m. Esos son los resultados que corresponden a n = 0, 1, 2, y 3 en la ecuación de distribución.
Las consecuencias de esta regla de distribución reafirman los resultados previos obtenidos por Christopher Alexander et al. (1977) y Léon Krier (1998). Nuestra ciudad hipotética se ha organizado en cinco regiones principales de alrededor de 5 km. (las “ciudades dentro la ciudad”). Ellas tienen 27 sub-regiones (localidades) de 1.7 km. de extensión. Finalmente, el tejido urbano es definido por 140 barrios diferentes (los “distritos, o “comunidades de 7,000 habitantes”) de cerca de 556 m de tamaño. Extrapolando las consecuencias que esto tiene en el tejido urbano se llega directamente a los patrones de Alexander “Mosaico de Subculturas” (Patrón 8), “El Límite de la Subcultura” (Patrón 13), y “Barrios Identificables” (Patrón 14).
Teóricamente, existirían muy pocas estructuras de tamaños intermedios a esos. Por supuesto, existen muchas estructuras urbanas de tamaños muy diferentes, pero esa distribución implica un vacío entre los tamaños más obvios. Esto significa una mejor definición de las estructuras de gran escala por medio de un borde identificable pero permeable — lo opuesto a la amorfa dispersión urbana de hoy en día que está fraccionada por todas partes por cercas y barreras. Si no encontramos que los tamaños anteriores se ajustan a la estructura urbana que estemos analizando, fácilmente se puede encontrar otra distribución utilizando nuevos parámetros de escala r y m . Lo mismo es válido para las escalas existentes. Si por razones prácticas necesitamos de estructuras, supongamos de 40 m. y 1 m., la jerarquía adoptada debe incluir esas escalas.
Otro punto es que la jerarquía se mantiene a medida que vamos disminuyendo de escalas. Por ejemplo, existirán 20,000 estructuras (edificios, espacios urbanos, espacios verdes) de 21 m., que corresponden a n = 6. Disminuyendo aún más la escala, la distribución pronostica 531,000 estructuras (componentes arquitectónicos, arbustos, y mobiliario urbano) de 2.3 m, que corresponden a n = 8, y 387 millones de estructuras de 2.8 cm. (ornamentación arquitectónica y detalles naturales), correspondientes a n = 12. Podríamos, por supuesto, acerarnos a escalas de 1 mm. y e incluso más pequeñas.
La importancia de esta discusión no radica en los resultados específicos dados arriba con fines únicamente explicativos, sino lo que representan. Una ciudad fractal (i.e., sin escala única fija) tiene componentes estructurales de todos los tamaños, desde el tamaño total de la ciudad hasta las dimensiones de las micro-estructuras de los materiales de construcción. Este enfoque conceptual unifica de una manera muy sencilla la planificación urbana, urbanismo, diseño del espacio urbano y la arquitectura, como diferentes escalas de una amplia disciplina. Quizás el aspecto más revolucionario de esta teoría es que pone en evidencia que la distribución de las estructuras construidas está sesgada de forma natural hacia la escala pequeña, deshaciendo de esta manera la parcialidad de la planificación del siglo XX hacia la gran escala.
APÉNDICE III: REPARANDO LA DISTRIBUCIÓN DE LA RED
Las telecomunicaciones encajan en de la jerarquía de los diferentes canales de movimiento e intercambio de información que tiene una ciudad (Drewe, 1999; 2000). Tener un número infinito de caminos electrónicos efectivos de longitud física nula coincide perfectamente con la Ley de Escalas en Potencia Inversa. Retomando la formula de la multiplicidad (Apéndice II) p = C x–m , con m entre 1 y 2. Cuando la longitud del camino x se vuelve cero, el número de p de caminos de longitud cero es infinita.
La introducción de las Tecnologías de la Información y Comunicación no repara la distribución de la longitud de los caminos físicos, debido a que es una red independiente. En casi todas las ciudades de hoy en día, existe un gran vacío en el lugar donde los caminos más cortos deberían estar. Este vacío en la distribución de la red puede ser únicamente cubierto por caminos que tomen como máximo 10 minutos en ser caminados. Paradójicamente, un análisis científico de las redes nos regresa directamente a la ciudad tradicional (Krier, 1998). En cualquier caso, existe un gran peligro, que la gente, convenientemente, aceptará las conexiones de longitud nula y no intentará reestablecer las conexiones peatonales que han sido perdidas.
A pesar de eso, las telecomunicaciones han alterado drásticamente la distribución de la longitud de los caminos hacia sus valores óptimos. Para ver esto, necesitamos analizar diferentes distribuciones de la red física. Un buen resultado que muestra esta diferencia es la longitud promedio de los caminos. En el primer caso, la ciudad modernista permite un número mínimo de las conexiones más largas, pero no de otro tipo. La distribución de la longitud de caminos tiene su punto más alto en algún múltiplo del tamaño de la ciudad xo, digamos (1/3) xo . Esto favorece fuertemente a los caminos más largos, y por lo tanto el agregar las telecomunicaciones satisface de forma parcial la necesidad fundamental de conexiones físicas en los rangos pequeños. Sin embargo, la distribución se mantiene distorsionada debido al gran vacío que hay donde los caminos más cortos deberían estar.
En el segundo caso, el modelo Erdös-Rényi de una ciudad conectada de manera aleatoria da el valor inferior correcto para la densidad óptima de caminos, pero de una longitud promedio irreal. Esta longitud tiene también su punto más alto en alguna fracción del tamaño más grande, como lo podría ser (1/3) xo (Barabási, 2002). Por el tamaño de la ciudad del automóvil actual, esta distribución representa la conectividad en automóvil, y por lo tanto menosprecia todas las conexiones peatonales.
El tercer caso, que es el que deseamos, es una ciudad sin escala única fija que sigue una Ley de Escalas en Potencia Inversa. La ciudad tiene la mayoría de sus conexiones en las escalas más pequeñas, de tal forma que los caminos más cortos son los que predominan. Denominemos el camino físico más corto — es decir la distancia desde un edificio conectado a otro edificio — como xmin. Por lo tanto, en este tipo de ciudad la longitud promedio de los caminos físicos va a ser algo alrededor de a 2 xmin . Esta longitud promedio es más corta por algunos ordenes de magnitud si se compara con las de los otros dos modelos. En teoría (y en la práctica) podríamos continuar con longitudes más cortas (y más numerosas). Tan solo en este caso sin escala única fija las telecomunicaciones se ajustan perfectamente con la distribución de las longitudes de los caminos.
Versión castellana del libro “Principles of Urban Structure” publicado por Techne Press, Amsterdam en 2005. Traducción del inglés hecha por Nuria Hernandez Amador, Oscar Mauricio Chamat Nuñez, María Fernanda Sánchez y Andrea Trietsch.
veredes, arquitectura y divulgación está colaborando con el autor para publicar algunos capítulos de su libro “Principles of Urban Structure“ traducidos gratis en la red, para el beneficio de los estudiantes hispanohablantes en todo el mundo. El libro en versión inglesa está publicado en Holanda, los EEUU y Nepal.
La Arquitectura de Información de las Ciudades | L. Andrew Coward – Nikos A. Salíngaros
Referencias
Albert, R., Jeong, H-W. and Barabási, A-L. (1999) “Diameter of the World-Wide Web”, Nature, Vol. 401, pp. 130.
Alexander, C. (1964) Notes on the Synthesis of Form, Cambridge, Massachusetts: Harvard University Press.
Alexander, C. (1965) “A City is Not a Tree”, Architectural Forum, Vol. 122, No. 1, pp. 58-61 and No. 2, pp. 58-62. Translated into many languages. Reprinted in: Design After Modernism, Edited by J. Thackara, Thames and Hudson, London (1988), pp. 67-84. Published electronically by RUDI (2001): <http://www.patternlanguage.com/archives/alexander1.htm>. Versión Castellana: ¿
Alexander, C. (1979) The Timeless Way of Building, Oxford University Press, New York. El Modo Intemporal de Construir, Barcelona: Editorial Gustavo Gili, 1981.
Alexander, C. (2002) The Nature of Order, Berkeley, California: The Center for Environmental Structure.
Alexander, C., Ishikawa, S., Silverstein, M., Jacobson, M., Fiksdahl-King, I. and Angel, S. (1977) A Pattern Language, New York: Oxford University Press. Un Lenguaje de Patrones, Barcelona: Editorial Gustavo Gili, 1980.
Alexander, C., Neis, H., Anninou, A. and King, I. (1987) A New Theory of Urban Design, New York: Oxford University Press.
Alexander, C., Silverstein, M., Angel, S., Ishikawa, S. & Abrams, D. (1975) The Oregon Experiment, Oxford University Press, New York. Une Expérience d’Urbanisme Démocratique, Paris: Éditions Seuil, 1976.
Allegrini, P., Barbi, M., Grigollini, P. and West, B.J. (1995) “Dynamical Model for DNA Sequences” Physical Review E, Vol. 52, pp. 5281-5296.
Allen, P. M. (1997) Cities and Regions as Self-Organizing Systems: Models of Complexity, Amsterdam: Gordon and Breach.
Bacon, E. N. (1974) Design of Cities, Harmondsworth, Middlesex, England: Penguin Books.
Barabási, A. L. (2002) Linked: The New Science of Networks, , Cambridge, Massachusetts: Perseus Publishing.
Batty, M. and Xie, Y. (1996) “Preliminary Evidence for a Theory of the Fractal City”, Environment and Planning A, Vol. 28, pp. 1745-1762.
Batty, M. and Longley, P. (1994) Fractal Cities, London: Academic Press.
Bollobás, B. (1985) Random Graphs, London: Academic Press.
Bonner, J. T., (1988) The Evolution of Complexity by Means of Natural Selection, Princeton, New Jersey: Princeton University Press.
Booch, G. (1991) Object Oriented Design, Redwood City, California: Benjamin/Cummings.
Bovill, C. (1996) Fractal Geometry in Architecture and Design, Boston: Birkhäuser.
Brand, S. (1995) How Buildings Learn, New York: Penguin Books.
Buchanan, M. (2002) Nexus: Small-worlds and the Groundbreaking Science of Networks, New York: W. W. Norton & Company.
Calder, W. A., (1984) Size, Function and Life History, Cambridge, Massachusetts: Harvard University Press.
Castells, M. (1989) The Informational City, Oxford: Blackwell.
Charles Prince of Wales (1989) A Vision of Britain, London: Doubleday.
Collins, G. R. and Collins, C. C. (1986) City Planning According to Artistic Principles, by Camillo Sitte, New York: Random House. [Der Städte-Bau, Carl Graeser Verlag, Vienna, 1901]
Coplien, J. O. and Schmidt, D., Ed. (1995) Pattern Languages of Program Design, Reading, Massachusetts: Addison-Wesley.
Courtois, P.-J. (1985) “On Time and Space Decomposition of Complex Structures”, Communications of the ACM, Vol. 28, pp. 590-603.
Coward, L. A. (1990) Pattern Thinking, New York: Praeger.
Coward, L. A. (2000) “A Functional Architecture Approach to Neural Systems”, Systems Research and Information Systems, Vol. 9, pp. 69-120.
Coward, L. A. (2001) “The Recommendation Architecture: Lessons from Large-Scale Electronic Systems Applied to Cognition”, Journal of Cognitive Systems Research, Vol. 2, pp. 111-156.
Cullen, Gordon (1961) The Concise Townscape, Oxford: Butterworth.
Dovey, K. (1990) “The Pattern Language and its Enemies”, Design Studies, Vol. 11, pp. 3-9.
Drewe, P. (1999) “In Search of New Concepts of Physical and Virtual Space”. In: Proceedings of the Conference: “Cities in the Global Information Society: an International Perspective”, University of Newcastle, Newcastle-upon-Tyne, November 22-24. Published in: M. Schrenk (ed.), Beitrage zum 5. Symposion “Computergestützte Raumplanung”—CORP 2000, Volume 1, Vienna University of Technology, pp. 37-44.
Drewe, P. (2000) “ICT and Urban Form: Planning and Design Off the Beaten Track”, Delft University of Technology, Design Studio ‘The Network City’, Faculty of Architecture.
Droege, P. (ed.), (1997) Intelligent Environments, Amsterdam: Elsevier.
Dupuy, G. (1991) L’Urbanisme Des Réseaux, Paris: Armand Colin.
Dupuy, G. (1995) Les Territoires de l’Automobile, Paris: Anthropos.
Edelman, G. M. and Tononi, G. (2000) A Universe of Consciousness, New York: Basic Books.
Eilenberger, G. (1985) “Freedom, Science, and Aesthetics”, in: Frontiers of Chaos, edited by: H. O. Peitgen and P. H. Richter (Bremen, Germany, MAPART, Forschungsgruppe Komplexe Dynamik der Universität), pp. 29-36.
Elia, M. M. (1996) Louis Henry Sullivan, New York: Princeton Architectural Press.
Erickson, T. (2000) “Lingua Francae for Design: Sacred Places and Pattern Languages”, in: Proceedings of the ACM Conference on Designing Interactive Systems 2000, New York: ACM Press, pages 357-368. [Brooklyn, New York, August 17-19, 2000]
Fathy, H. (1973) Architecture for the Poor, Chicago: University of Chicago Press.
Fischler, M. A. and Firschein, O. (1987) Intelligence: The Eye, the Brain, and the Computer, Reading, Massachusetts: Addison-Wesley.
Frankhauser, P. (1994) La Fractalité des Structures Urbaines, Paris: Anthropos.
Friedman, A. (1997) “Design for Change: Flexible Planning Strategies for the 1990s and Beyond”, Journal of Urban Design, Vol. 2, pp. 277-295.
Gabriel, R. (1996) Patterns of Software. New York: Oxford University Press.
Gamma, E., Helm, R., Johnson, R. and Vlissides, J. (1995) Design Patterns, Reading, Massachusetts: Addison-Wesley.
Garlan, D., Allen, R. and Ockerbloom, J. (1995) “Architectural Mismatch, or Why it’s hard to build systems out of existing parts”. In: Proceedings of the Seventeenth International Conference on Software Engineering, IEEE Computer Society, New York: ACM Press, 179-185. Revised version in: IEEE Software, Vol. 12 (November 1995), pp. 17-26.
Garnsworthy, A. and O’Connor, K. (1997) “Knowledge-Based Manufacturing and Regional Change”, in: Intelligent Environments, edited by: P. Droege, Amsterdam: Elsevier, pp. 87-97.
Gehl, J. (1987) Life Between Buildings, New York: Van Nostrand Reinhold. [reprinted by Arkitektens Forlag, Copenhagen, Denmark, Fax 45 33912770]
Gleick, J. (1987) Chaos, New York: Viking/Penguin.
Graham, S. and Marvin, S. (1996) Telecommunications and the City, London: Routledge.
Graham, S. and Marvin, S. (2001) Splintering Urbanism, London: Routledge.
Greenberg, M. (1995) The Poetics of Cities, Columbus: Ohio State University Press.
Habraken, N. J. (1998) The Structure of the Ordinary, Cambridge, Massachusetts: MIT Press.
Hallowell, E. M. (1999) “The Human Moment at Work”, Harvard Business Review (January-February 1999), pp. 58-66.
Hanson, B. and Younés, S. (2001) “Reuniting Urban Form and Urban Process”, Journal of Urban Design, Vol. 6: pp. 185-209.
Hester, R. T. (1993) “Sacred Structures and Everyday Life: A Return to Manteo, North Carolina”, in: Dwelling, Seeing, and Designing, Edited by: David Seamon, New York: State University of New York Press, pp. 271-297.
Heylighen, F. (1999) “Collective Intelligence and its Implementation on the Web”, Computational and Mathematical Organization Theory, Vol. 5: pp. 253-280.
Highsmith, J. A. (2000) Adaptive Software Development, New York: Dorset House Publishing.
Hillier, W. R. G. and Hanson, J. (1984) The Social Logic of Space, Cambridge: Cambridge University Press.
Hillier, B. (1996) Space is the Machine, Cambridge: Cambridge University Press.
Hillier, B. (1997) “Cities as Movement Economies”, in: Intelligent Environments, Edited by: P. Droege, Amsterdam: Elsevier, pp. 295-342. Appears as Chapter 4 of: Bill Hillier (1996) Space is the Machine, Cambridge: Cambridge University Press.
Hillier, B. (1999) “The Hidden Geometry of Deformed Grids”, Environment and Planning B, Vol. 26, pp. 169-191.
Hillis, W. Daniel. (1992) “Co-Evolving Parasites Improve Simulated Evolution as an Optimization Procedure”. In: Artificial Life II, edited by C. G. Langton, C. Taylor, J. D. Farmer & S. Rasmussen, Reading, Massachusetts: Addison-Wesley, pp. 313-324.
Hillis, W. D. (1998) The Pattern on the Stone, New York: Basic Books.
Jacobs, J. (1961) The Death and Life of Great American Cities, New York: Vintage Books.
Johnson, S. (2001) Emergence, New York: Scribner.
Kauffman, S. (1995) At Home in the Universe, New York: Oxford University Press.
Kaye, B. H. (1994) A Random Walk Through Fractal Dimensions, 2nd Edition, Weinheim, Germany: VCH Verlagsgesellschaft.
Krier, L. (1998) Architecture: Choice or Fate, Windsor, Berkshire, England: Andreas Papadakis. French translation: Architecture: Choix ou Fatalité, Paris: Norma, 1996. Italian translation: Architettura: Scelta o Fatalità, Roma-Bari: Editori Laterza, 1995.
Krier, R. (1979) Urban Space, New York: Rizzoli.
Kunstler, J. H. (1996) Home From Nowhere, New York: Simon & Schuster.
Light, J. (1999) “From City Space to Cyberspace”. In: M. Crang, P. Crang, and J. May (eds.), Virtual Geographies, London: Routledge, 1999, pp. 109-130.
Lotka, A. J. (1926) “The Frequency Distribution of Scientific Productivity”, J. Washington Academy of Sciences, Vol. 16, pp. 317-323.
Lotka, A. J. (1956) Elements of Mathematical Biology, New York: Dover.
Lozano, E. E. (1990) Community Design and the Culture of Cities, Cambridge: Cambridge University Press.
Lynch, K. (1960) The Image of the City, Cambridge, Massachusetts: MIT Press.
Madanipour, A. (1996) Design of Urban Space, Chichester, England: John Wiley.
Makse, H. A., Havlin, S. and Stanley, H. E. (1995) “Modelling Urban Growth Patterns”, Nature, Vol. 377, pp. 608-612.
Mandelbrot, B. B. (1983) The Fractal Geometry of Nature, New York: Freeman.
Mehaffy, M. W. and Salingaros, N. A. (2002) “The End of the Modern World”, PLANetizen, January. < http://www.planetizen.com/node/38>. Reprinted by Open Democracy, February 2002.
Meier, R. L. (1962) A Communications Theory of Urban Growth, Cambridge, Massachusetts: MIT Press.
Mesarovic, M. D., Macko, D. and Takahara, Y. (1970) Theory of Hierarchical Multilevel Systems, New York: Academic Press.
Mikiten, T. M., Salingaros, N. A. and Yu, H. (2000) “Pavements as Embodiments of Meaning for a Fractal Mind”, Nexus Network Journal, Vol. 2, pp. 63-74. Capítulo 7 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Miller, G. A. (1956) “The Magical Number Seven Plus or Minus Two: Some Limits on Our Capacity for Processing Information”, The Psychological Review, Vol. 63, pp. 81-97.
Miller, J. G. (1978) Living Systems, New York: McGraw-Hill.
Moughtin, C. (1992) Urban Design: Street and Square, Oxford: Butterworth.
Moughtin, C, Oc, T. and Tiesdell, S. (1995) Urban Design: Ornament and Decoration, Oxford, England: Butterworth.
Newman, P. and Kenworthy, J. (1999) Sustainability and Cities, Washington D.C.: Island Press.
Nyikos, L., Balazs, L. and Schiller, R. (1994) “Fractal Analysis of Artistic Images: From Cubism to Fractalism”, Fractals, Vol. 2, pp. 143-152.
Pareto, V. (1897) Cours d’Economie Politique, Lausanne, Switzerland.
Parnas, D. L., Clements, P. C. and Weiss, D. M. (1985) “The Modular Structure of Complex Systems”, IEEE Transactions on Software Engineering, SE-11, pp. 259-266.
Passioura, J. B. (1979) “Accountability, Philosophy, and Plant Physiology”, Search (Australian Journal of Science), Vol. 10 No. 10, pp. 347-350.
Paumier, C. B. (1988) Designing the Successful Downtown, Washington, DC: Urban Land Institute.
Peters, R. H. (1983) The Ecological Implications of Body Size, Cambridge: Cambridge University Press.
Portugali, J. (2000) Self- organization and Cities, Heidelberg: Springer-Verlag.
Pree, W. (1995) Design Patterns for Object-Oriented Software Development, Reading, Massachusetts: Addison-Wesley.
Ribeiro, G. (1997) “An Ecological Approach to the Study of Urban Spaces: the Case of a Shantytown in Brasilia”, Journal of Architectural and Planning Research, Vol. 14, pp. 289-300.
Robertson, L. (1995) “A New Theory for Urban Design”, Urban Design Quarterly, Vol. 56, pp. 11-13.
Sahal, D. (1981) Patterns of Technological Innovation, Reading, Massachusetts: Addison-Wesley.
Salingaros, N. A. (1995) “The Laws of Architecture from a Physicist’s Perspective”, Physics Essays , Vol. 8, pp. 638-643. Capítulo 1 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006). Traducción en español: “Las Leyes de la Arquitectura desde la Perspectiva de un Físico”, El Hombre y la Máquina, No 16 (Abril de 2001) páginas 12-23. Republicado en: La Simetria (Febrero de 2002).
Salingaros, N. A. (1997) “Life and Complexity in Architecture From a Thermodynamic Analogy”, Physics Essays, Vol. 10, pp. 165-173. Capítulo 5 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (1998) “A Scientific Basis for Creating Architectural Forms”, Journal of Architectural and Planning Research, Vol. 15, pp. 283-293. Capítulo 2 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (1999) “Architecture, Patterns, and Mathematics”, Nexus Network Journal, Vol 1, pp. 75-85. Capítulo 6 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (2000) “Hierarchical Cooperation in Architecture, and the Mathematical Necessity for Ornament”, Journal of Architectural and Planning Research, Vol. 17, pp. 221-235. Capítulo 3 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (2001) “Fractals in the New Architecture”, Archimagazine. Reprinted in Katarxis No. 3 (September 2004). Traduzione in italiano: “I Frattali Nella Nuova Architettura”, Archimagazine (2001).
Salingaros, N. A. (2004) “Charles Jencks and the New Paradigm in Architecture”, Part 2 of Anti-Architecture and Deconstruction, Umbau-Verlag, Solingen, 2004, pp. 41-55. Shortened version in Chaos & Complexity Letters, Vol. 1, No. 2 (2004), pp. 101-106. Capítulo 3 de: Anti-Architecture and Deconstruction, Solingen, Germany: Umbau-Verlag (2007).
Salingaros, N. A. and Mikiten, T. M. (2002) “Darwinian Processes and Memes in Architecture: A Memetic Theory of Modernism”, Journal of Memetics—Evolutionary Models of Information Transmission, Vol. 6. Reprinted in: DATUTOP Journal of Architectural Theory, Vol. 23 (2002), pp. 117-139. Capítulo 10 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Shannon, C. E. and Weaver, W. (1949) The Mathematical Theory of Communication, Urbana: University of Illinois Press.
Simon, H. A. and Ando, A. (1961) “Aggregation of Variables in Dynamic Systems”, Econometrica, Vol. 29, pp. 111-138.
Simon, H. A. (1962) “The Architecture of Complexity”, Proceedings of the American Philosophical Society, Vol. 106, pp. 467-482. Reprinted in: Herbert A. Simon, The Sciences of the Artificial, Cambridge, Massachusetts: MIT Press, 1969, pp. 84-118.
Sörgel, H. (1918) Einführung in die Architektur-Ästhetik, Munich: Piloty & Loehle.
Steen, L. A. (1988) “The Science of Patterns”, Science, Vol. 240, pp. 611-616.
Stringer, P. (1975) “The Myths of Architectural Creativity”, Architectural Design, Vol. 45, pp. 634-635.
Van der Ryn, S. and Cowan, S. (1996) Ecological Design, Washington, D.C.: Island Press.
Ward, V. and Holtham, C. (2000) “The Role of Private and Public Spaces in Knowledge Management”. In: Knowledge Management: Concepts and Controversies, 10-11 February 2000, University of Warwick, Coventry, UK.
Watts, D. J. and Strogatz, S. H. (1998) “Collective Dynamics of ‘Small-World’ Networks”, Nature, Vol. 393, pp. 440-442.
Weaver, W. (1948) “Science and Complexity”, American Scientist, Vol. 36, pp. 536-544.
West, B. J. and Deering, W. (1994) “Fractal Physiology for Physicists: Lévy Statistics”, Physics Reports, Vol. 246, Nos. 1&2, pp. 1-100.
West, B. J. and Deering, B. (1995) The Lure of Modern Science, Singapore: World Scientific.
West, B. J. and Salk, J. (1987) “Complexity, Organization and Uncertainty”, European J. Operations Research, Vol. 30, pp. 117-128.
West, B. J. and Shlesinger, M. (1990) “The Noise in Natural Phenomena”, American Scientist, Vol. 78, pp. 40-45.
Whyte, W. H. (1980) The Social Life of Small Urban Spaces, Washington, D.C.: The Conservation Foundation.
Wiedenhoeft, R. (1981) Cities for People, New York: Van Nostrand Reinhold.
Willis, J. C., (1922) Age and Area: A Study in Geographical Distribution and Origin of Species, Cambridge, England: Cambridge University Press.
Zipf, G. K. (1949) Human Behavior and the Principle of Least Effort, Cambridge, Massachusetts: Addison-Wesley.






