Capítulo 1 del libro «Principios de la Estructura Urbana», 2005, de Nikos A. Salíngaros
Este capítulo identifica procesos fundamentales detrás del diseño urbano. Las reglas se derivan de principios conectivos en la teoría de complejidad, el reconocimiento de patrones, y la inteligencia artificial. Cualquier vecindad urbana se puede descomponer en nodos de la actividad humana y sus interconexiones. Las conexiones entonces se tratan como problema matemático (aquí de una manera cualitativa). El diseño urbano es más acertado cuando establece un cierto número (mínimo) de conexiones entre los nodos de actividad. Las matemáticas sí mismas dependen sobre establecer relaciones entre las ideas; esta capacidad es un componente central de la inteligencia de los seres humanos. La creación del ambiente construido es conducida por las fuerzas análogas a las que nos conduzcan a hacer matemáticas.
Introducción
La arquitectura y el diseño urbano han resistido hasta ahora una formulación científica en parte debido a su complejidad subyacente. Las mismas razones retrasaron los fundamentos científicos de la medicina, que hasta hace poco tiempo estuvieron basados tanto en la superstición como en la ciencia. Los esfuerzos del pasado de plantear el planeamiento urbano en términos teóricos — identificando los procesos que dan lugar a formas observadas — han tenido poco impacto en el desarrollo real. Existen tres notables y recientes acercamientos: (1) el trabajo pionero de Christopher Alexander (Alexander, 1964; 1965; 1998; Alexander, Ishikawa et al., 1977; Alexander, Neis et al., 1987) que proporciona la espina dorsal de este escrito; (2) el marco de patrones urbanos como fractales acentúa sus jerarquías y micro-estructura ligadas (Batty y Longley, 1994; Batty y Xie, 1996); (3) la formulación de preguntas urbanas en términos de relaciones y movimientos que da luz a las fuerzas que gobiernan el crecimiento de una ciudad (Hillier, 1996; Hillier y Hanson, 1984). Aquí nos centraremos en los procesos conectivos como base del tejido urbano.
Un componente central del intelecto humano es la capacidad de establecer conexiones. Las conexiones entre las ideas dan lugar a una mejor comprensión de la naturaleza. El reconocimiento de los patrones que se ocultan al observador ocasional es la llave del desarrollo científico. Estudios neurológicos demuestran que la mayor parte del cerebro está involucrado en la percepción visual, lo que sugiere que la inteligencia ha evolucionado para apoyar el proceso perceptivo (Fischler y Firschein, 1987). La capacidad de establecer conexiones se aplica tanto a la percepción visual y a procesos más abstractos, menos obvios, y se ha desarrollado hasta tal punto que marca la diferencia del éxito de la especie humana para dominar a las otras especies animales. Estableceré una analogía entre las conexiones mentales y las conexiones entre los elementos urbanos que dan lugar a una ciudad o a una pieza de paisaje urbano.
El tejido urbano es una estructura de complejidad organizada que existe sobre todo en el espacio entre los edificios (Gehl, 1987). Cada edificio incluye y abarca uno o más nodos de actividad humana. Los nodos externos van desde los que están totalmente expuestos hasta los que tienen varios grados de resguardo parcial. La red urbana está conformada por todo el exterior y por los elementos conectivos como áreas peatonales y verdes, muros libres, sendas peatonales y caminos que van desde una ciclopista (ciclovía) hasta una autopista. Observaciones empíricas refuerzan el concepto de que mientras más fuertes son las conexiones y más subestructura tenga la red, una ciudad tiene más vida (Alexander, 1965, Gehl, 1987).
La exposición comienza estableciendo tres principios generales. Estos a su vez se desarrollan en una teoría de la red urbana, que proporciona reglas prácticas de aplicación. Se discute la necesidad de diversos tipos de conexiones. Un resultado matemático en la irregularidad de las conexiones demuestra por qué las trayectorias rectas que parecen regulares en un plan son generalmente inadecuadas, y no funcionan por otras razones (figura 1). Un modelo usado en la biología molecular que organiza elementos por pares para alcanzar la unión se revisa después. Esto demuestra que la red urbana no puede existir sin un mínimo (y muy grande) número de conexiones.
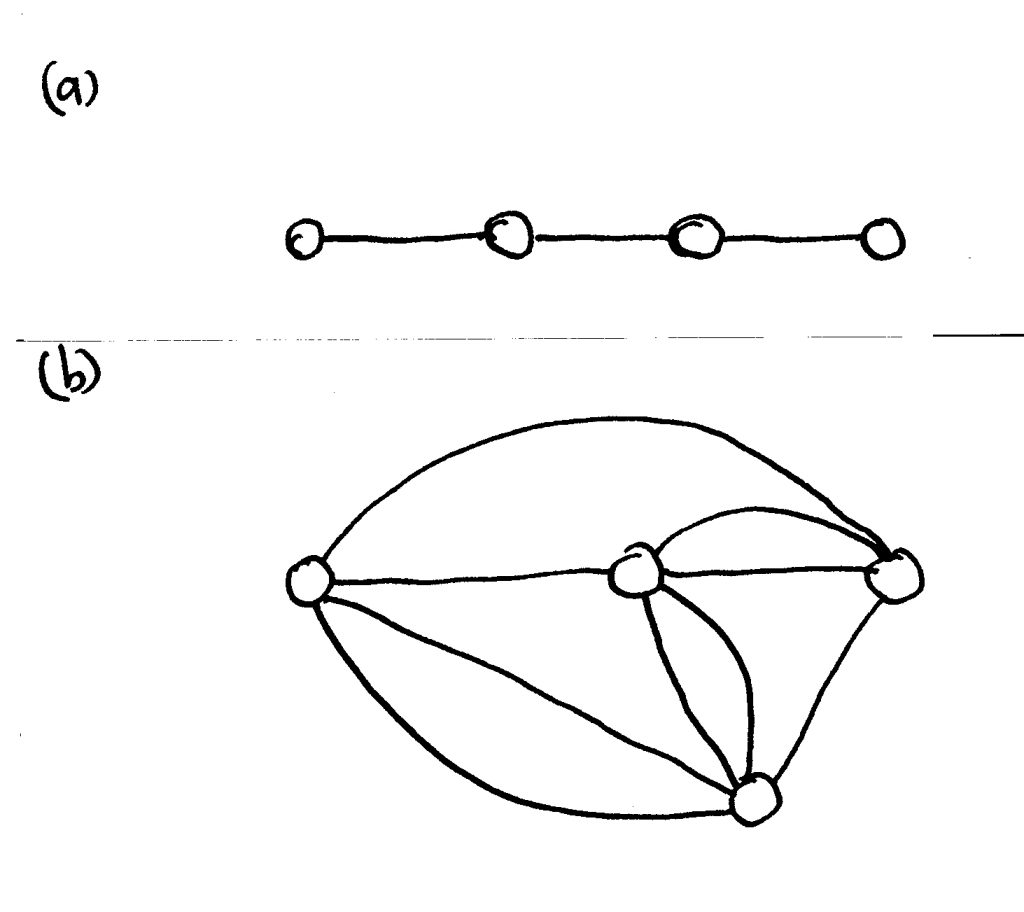
Después, se examina cómo se logra la complejidad en una ciudad. Si no hay suficiente complejidad, la ciudad está muerta; si tiene complejidad sin la suficiente organización, una ciudad llega a ser caótica e invivible. Uno de los impulsos fundamentales de la humanidad a través del tiempo ha sido elevar el nivel de complejidad organizada. Una de las ideas principales de este trabajo es que una ciudad imita los procesos humanos del pensamiento, y que ambas dependen de establecer conexiones. Esta analogía explica y hace menos misterioso por qué construimos cosas complejas.
La segunda mitad de este capítulo enumera algunas aplicaciones de la teoría. Los caminos y las trayectorias son las conexiones de la red, y las examinamos a través de su estructura y jerarquía apropiada. Los consejos prácticos a los planificadores se enfocan a cómo construir mejores colonias. Hay acciones que se pueden tomar para regenerar colonias existentes con un esfuerzo mínimo. Se menciona cómo puede ser mejorada un área comercial al menudeo. Finalmente, se discute el uso apropiado de límites. Existen muchas situaciones donde se necesita inhibir o controlar las conexiones en vez de establecerlas en todas las escalas. En una ciudad sana, es necesario desconectar dos regiones que se dañen mutuamente.
Principios estructurales de la red urbana
El proceso que genera la red urbana puede ser resumido en términos de tres principios. Aunque no son exhaustivos, son completamente generales, y este escrito describirá cómo se traducen en reglas prácticas de diseño para situaciones específicas. Todo tiene que ver con conexiones y la topología de las mismas. Los tres principios pueden ser indicados de la manera siguiente:
(1) Nodos. La red urbana se basa en nodos de actividad humana cuyas interconexiones conforman la red. Existen distintos tipos de nodos: habitación, trabajo, parques, tiendas, restaurantes, iglesias, etc. Los elementos naturales y arquitectónicos sirven para reforzar los nodos de actividad humana y sus trayectorias de conexión. La red determina el espacio y la organización en planta de los edificios, no viceversa. Los nodos que están muy separados no se pueden conectar con una senda peatonal.
(2) Conexiones. Los pares de conexiones se forman entre los nodos complementarios, no entre nodos del mismo tipo. Las trayectorias peatonales consisten en tramos cortos y rectos entre los nodos; ninguna sección debe exceder cierta longitud máxima. Para acomodar conexiones múltiples entre dos puntos, algunas trayectorias deben ser necesariamente curveadas o irregulares. Muchas conexiones que coinciden sobrecargan la capacidad del canal de conexión. Las trayectorias acertadas son definidas por el borde entre regiones planas que contrastan y forman a lo largo de los límites.
(3) Jerarquía. Cuando se permite, la red urbana se auto-organiza creando una jerarquía ordenada de conexiones en muchos y diferentes niveles de escala. Se vuelve múltiplemente conectada pero no caótica. El proceso de organización sigue un estricto orden: empieza con las escalas menores (sendas peatonales), y progresa hacia escalas superiores (calles de capacidad creciente). Si no existe cualquiera de los niveles de conectividad, la red se vuelve patológica. Una jerarquía rara vez se puede establecer toda al mismo tiempo.
Estos principios se sugieren por los resultados en matemáticas. Los términos no son nuevos (Lynch, 1960), pero su uso aquí es más específico que en el trabajo de autores anteriores. Como resultado, las conclusiones son más fuertes y las soluciones permitidas están más restringidas. El crecimiento urbano ha seguido reglas similares a través de casi toda la historia. La planeación urbana en este siglo, sin embargo, incorpora reglas que son, en muchos casos, el opuesto a los principios descritos anteriormente. Mostraré cómo la adopción de estilos arbitrarios de diseño, que contradicen principios matemáticos relevantes, destruye la red urbana (Batty y Longley, 1994).
Conexiones en arquitectura y diseño urbano
La arquitectura ata elementos y espacios estructurales para alcanzar la cohesión. Las conexiones en diseño urbano ligan entre ellos a tres tipos distintos de elementos: elementos naturales, nodos de actividad humana y elementos arquitectónicos. Ejemplos de elementos naturales incluyen ríos, un grupo de árboles, una grande roca caída o un pedazo de pasto. Las actividades humanas definen nodos tales como un lugar de trabajo, una residencia, un conjunto de tiendas o un sitio para sentarse y beber una taza de café. Los elementos arquitectónicos incluyen todo lo que los seres humanos construyan para conectar elementos naturales y refuercen sus nodos de actividad.
Conectando nodos de actividad humana.
Los nodos urbanos no están totalmente definidos por las estructuras como un gran edificio o un monumento. Éstos pueden ser más efímeros o modestos, como un puesto de tacos o una banca sombreada. Los nodos deben atraer a la gente por alguna razón, entonces, un edificio o un monumento será un nodo solo si ahí existe una actividad bien definida. Los grandes edificios y los monumentos que también proveen un nodo para la actividad humana actúan como foco para las trayectorias, y tienen éxito. En contraste, los sitios arquitectónicos que no refuerzan la actividad humana, fracasan, se aíslan ellos mismos de la red urbana.
Hay que hacer una distinción entre las conexiones visuales y las trayectorias que conectan el movimiento físico de las personas. Como enfatizó Kevin Lynch (1960), y desarrolló después Bill Hillier (Hillier, 1996; Hillier y Hanson, 1984), las conexiones visuales son necesarias para la orientación, y para la creación de una imagen coherente del ambiente urbano. Sin embargo, como no siempre coinciden con las trayectorias y calles, no son el tema principal de este escrito. La interdependencia entre conexiones visuales y trayectorias es muy compleja y será retomada en otra ocasión.
El número y tipo de conexiones entre nodos de actividad humana es (o debería ser) increíblemente grande. Desde los años ‘40, los planeadores urbanos han seguido reglas cuyo objetivo es crear un plan con un mayor grado de regularidad geométrica, al menos en los centros urbanos. (Alexander, 1965; Batty y Longley, 1994; Gehl, 1987). Esto está basado casi siempre en ideas estilísticas arbitrarias que frustran tanto a los nodos como a las conexiones. Concentrándose en la simplicidad visual de formas totales, los nodos humanos son ignorados hasta que es demasiado tarde para definirlos apropiadamente. Como resultado de esto, las actividades humanas tienen que encajar en una matriz construida previamente que nunca podrá acomodarlas (ver figura 1).
Los elementos arquitectónicos se conectan visualmente entre ellos a la distancia a través de simetrías, similitudes y formas intermedias (Salingaros, 1995). Sin embargo, existe una diferencia básica entre las conexiones arquitectónicas y las humanas. Las conexiones funcionales entre nodos de actividad humana no son favorables en términos de simetrías porque esos patrones son sumamente complejos. Por esta razón, se tiende a ignorarlos siempre que una ciudad es planeada basándose en términos visuales. Lo que en realidad determina totalmente la forma de una red urbana funcional es la complejidad organizada y no los términos visuales (ver figura 1). La organización combina la conectividad múltiple con el orden jerárquico. Una pieza de red urbana puede verse organizada pero estar desconectada. Por el contrario, otra pieza puede verse desorganizada en planta, pero estar altamente conectada y ser funcional.
Las trayectorias de conectividad son múltiples e irregulares
Cada elemento en un conjunto urbano tiene un significado en la medida que se relacione con las actividades humanas. Los diferentes nodos de una red urbana se conectan mediante un complejo proceso de organización. Las conexiones permiten llegar fácilmente a cualquier punto, y preferentemente por muchas y distintas trayectorias; la imagen que da un barrio a los pasajeros de un avión es por mucho irrelevante. Un ambiente urbano ordenado que está fuertemente conectado casi siempre se ve irregular desde el aire (Gehl, 1987; Hillier, 1996) (Figuras 1 y 2). La regularidad geométrica en planta, aunque es útil como principio de organización, no es necesariamente experimentada así a nivel de piso (Batty y Longley, 1994).
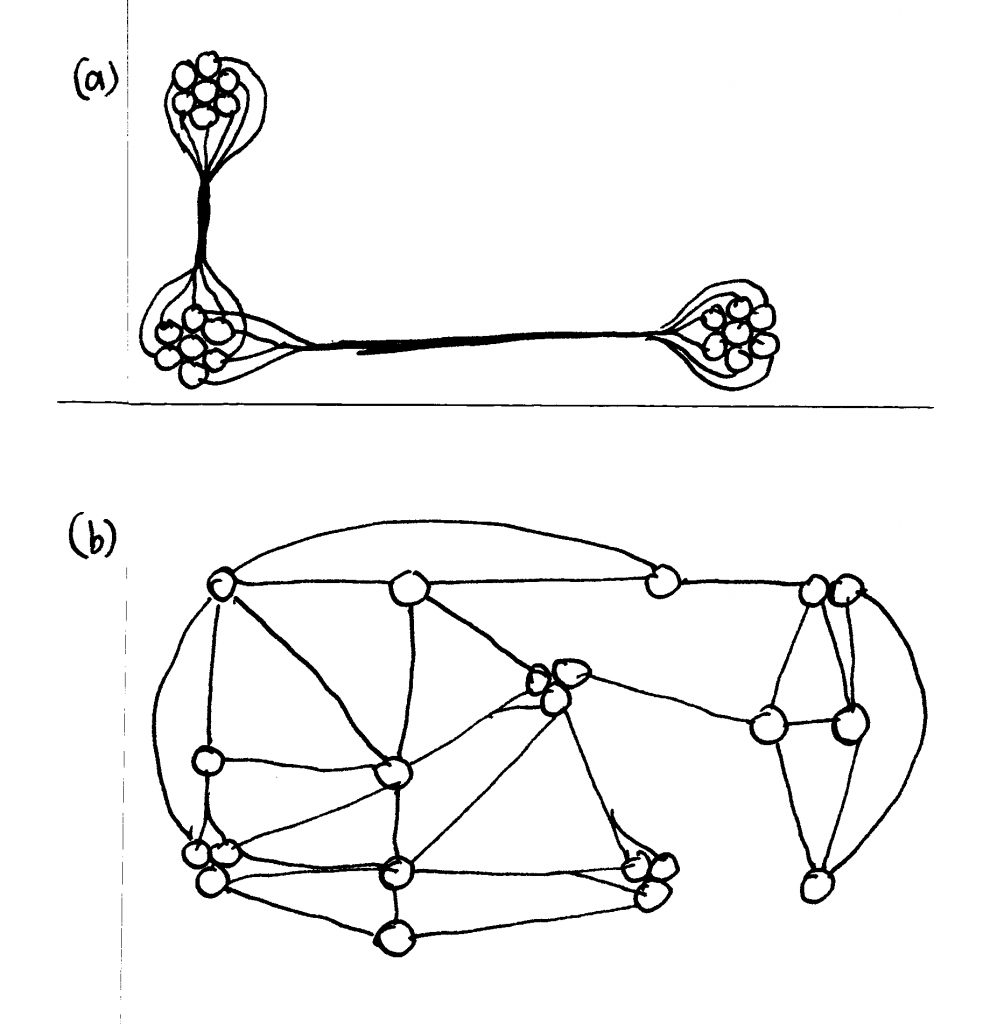
Un teorema matemático dice que dos puntos pueden estar conectados por una línea recta sólo de una manera, pero pueden estar conectados por líneas curvas en un número infinito de formas. Si queremos el máximo posible de conexiones entre nodos urbanos, no podemos insistir en conexiones rectas en una retícula Cartesiana (Hipodámica). Como expuso Camilo Sitte, y puede ser verificado por cualquier observador, las calles curvas de las ciudades medievales son sumamente placenteras. Este efecto trató de imitarse en los desarrollos suburbanos con calles curvas, pero esos ejemplos recientes tienen conexiones insuficientes, tanto internas como externas.
La idea modernista de separación de funciones ha dejado como consecuencia, la distinción entre las regiones urbanas y suburbanas en lo que se refiere a apariencias estilísticas opuestas (y arbitrarias). La regularidad geométrica es la regla en las regiones urbanas. El estilo opuesto se aplica a las áreas suburbanas. En los ‘60 se puso de moda la construcción de desarrollos habitacionales con calles curvas. Las conexiones se reducen en gran cantidad teniendo calles y callejones sin salida. Este enfoque tiene como meta el aislamiento de los nodos, que evita la formación de la red urbana. Hemos imitado un estilo visual superficialmente (la irregularidad de los planes medievales) malentendiéndolo y reproduciéndolo perdiendo la esencia de la solución original (alto grado de conectividad peatonal).
La teoría de la conectividad múltiple es motivada y respaldada por un resultado principal de física. En la formulación de trayectoria-integral de la mecánica quántica de Feynman, la interacción entre dos objetos puede describirse como la suma de las interacciones sobre todas las trayectorias posibles. Para calcular la fuerza total de interacción, se consideran todas las posibles trayectorias que unen dos puntos, con un peso apropiado de acuerdo a la probabilidad de que ocurran. Después se integran todas las trayectorias para obtener la fuerza total de interacción. Por analogía, si queremos que cada nodo de la red urbana esté fuertemente conectado, sólo es posible mediante la multiplicidad de trayectorias irregulares. (El metro de Tokio nos da un ejemplo claro de muchas redes en capas, superpuestas una encima de la otra).
Sin embargo, no es necesario ni deseable que todas las calles tengan curvas. En principio, no hay nada malo con un plan de retícula regular, y provee obvias ventajas de organización. Lo que es criticable es la rigidez de su aplicación más común, que frecuentemente limita el número de conexiones. Es posible sobreponer otra retícula con un ángulo para crear diagonales; esto proveerá conectividad múltiple. Como se explica luego en este capítulo, se debe permitir que las trayectorias se entrecrucen en una retícula de calles rectangular.
Se podría conservar la claridad de una retícula rectangular y disminuir la fineza de sus subdivisiones. El cortar en la retícula con trayectorias paralelas (de vehículos o peatonales) crea conexiones en forma de cruz, y si son vehiculares, se disminuye el tamaño de la cuadra. En nuestros días, las cuadras grandes en las ciudades y suburbios frustran la conectividad cruzada porque no permiten la creación de trayectorias internas. En el caso de los grandes núcleos comerciales, residenciales o complejos de edificios gubernamentales, es necesario cortar las trayectorias a través de cada grupo, si no, esa región estará aislada de la trama urbana. Las grandes planchas grises de estacionamiento son “tierra de nadie” para el peatón, así que las trayectorias deben ser protegidas por pavimentos elevados y baldaquinos. Las conexiones individuales a través de una región urbana están compuestas de muchos segmentos más pequeños y son múltiples e irregulares.
La estabilidad contra la pérdida de conexiones
La sugerencia puede basarse en que las ciudades funcionales complejas son las que tienen un alto grado de redundancia en el uso del concepto de la red. Si se consiguen cada vez más formas de atravesar una ciudad a través de sus nodos, y después se interrumpe alguna unión entre dos de ellos, la ciudad todavía trabaja. Esto funciona como el cerebro (Fischler y Firschein, 1987). Si se pierden algunas conexiones entre las neuronas (por una lesión, intervención quirúrgica o como resultado natural de envejecimiento), el cerebro todavía trabaja en su mayoría. Esto sucede por la cantidad tan alta de redundancia que los mensajes encuentran a través de él. Si se pone esto en contraste con las máquinas que se detienen totalmente cuando se daña un circuito de menor importancia. Esta noción de estabilidad contra el hecho de cortar una red es complementaria a las ideas más recientes en el umbral de la complejidad. Ya existe investigación sobre la estabilidad de las redes de comunicación en donde cada línea tiene cierta probabilidad de fallar, que se aplica directamente al tejido urbano.
Evitar la sobrecarga de los canales
Existen razones funcionales para la conectividad múltiple. Las trayectorias comúnmente se unen dentro de un canal (ver figura 2). Cuando las conexiones son todas del mismo tipo, compiten entre ellas y exceden la capacidad de flujo del canal. La singularidad (cantidad matemática que se vuelve infinita) se manifiesta tanto en sentido peatonal como en un embotellamiento vehicular. En los casos donde coinciden conexiones de distintos tipos, las conexiones más débiles desaparecen totalmente. Por ejemplo, las sendas peatonales o las ciclopistas no pueden coexistir con una avenida. Las conexiones de muy distintos niveles pueden cruzarse pero no coincidir.
El “modelo de juguete” de la biología evolutiva
La nueva ciencia de la complejidad sostiene nuestras propuestas de diseño urbano. Como resultado de la teoría de los gráficos aleatorios aplicada en un modelo biológico evolutivo se ilustra lo que realmente pasa cuando se crea una red urbana organizada. Ésta imita el proceso de la construcción en la historia. Suponiendo que se conectan todos los elementos de un escenario urbano. Se puede tratar de lograr la máxima organización haciendo ajustes a los componentes: moviéndolos y modificándolos de modo que los nodos y los elementos arquitectónicos se conecten entre ellos en la distancia. El objetivo es siempre la creación de conexiones.
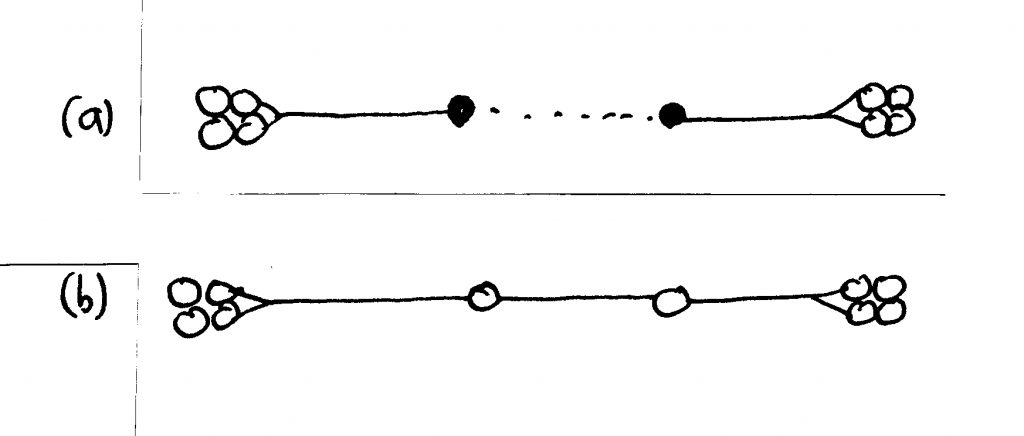
La organización se puede estudiar en términos de ligas por pares. Consideramos N elementos que son inicialmente independientes. Escoge cualquier par al azar y conéctalos, repitiendo este proceso en todos los pasos. Cada vez se establece una conexión y de este modo se crean muchas cadenas pequeñas. La longitud de la cadena más grande inicialmente será muy pequeña e irá creciendo lentamente. En algún punto, dos o más cadenas se unirán. Hasta al paso N/2, los elementos están ligados en su mayoría en pares que son independientes unos de otros. Cuando el número de conexiones por pares excede el paso N/2 , cadenas pequeñas empiezan a conectarse entre ellas, y a un paso entre N/2 y (N/2) lnN, muchos elementos estarán unidos para formar una cadena gigante y múltiplemente conectada (Bollobás, 1965; Kauffman, 1995) (Figura 3). Mientras más grande sea el sistema, la fusión será más repentina. El sistema ha experimentado una transición de fase de un estado desorganizado a uno organizado. Más adelante, el acoplamiento por parejas incrementará el tamaño de su cadena más grande, pero sólo a través de pequeños incrementos y hasta que haya conectado más del 80% de sus elementos (Bollobás, 1985; Kauffman, 1995).
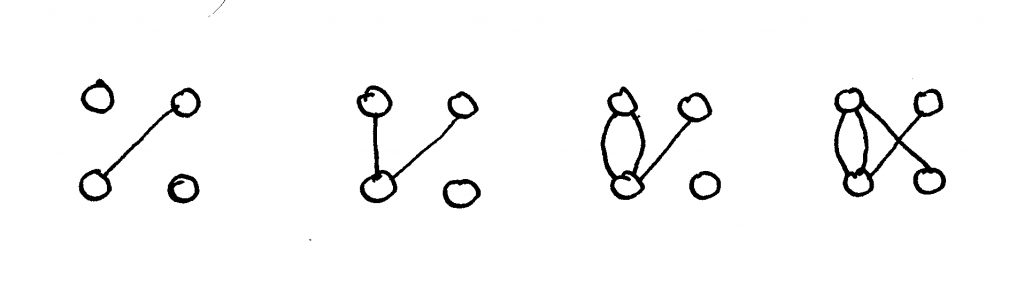
Este resultado se aplica al diseño urbano de la siguiente manera. El proceso de planeación puede realizarse en un modelo por computadora o puede desarrollarse gradualmente en la construcción a través de los años. El incremento en la conexión de los nodos deriva un mejoramiento perceptible en la organización de toda la estructura. Lo que resulta es sorprendente y se relaciona a una transición de fase. El punto se alcanza cuando casi todo está fusionado: en este momento la organización ha sido alcanzada. De este momento en adelante, cada observador experimentará el conjunto como un todo unido.
Hablando de complejidad, siempre existe una transición de fase; en las ciudades, cuando el número de conexiones entre distintos nodos o lugares adquiere cierto orden, una gran proporción del total de nodos se conecta de repente. Esta explicación puede usarse para clasificar a las ciudades, y a ciertas de ellas idealizadas y su geometría, y hasta podrá relacionarse con la función de la ciudad. Este modelo se parece, por supuesto, a un modelo de filtración utilizado para el flujo del agua: cuando aparece el número de hoyos adecuado en un medio poroso, el agua pasa de repente a través de él. Igualmente, cuando el número suficiente de árboles se une para formar un bosque y comienza un incendio forestal, el fuego se expande a través del bosque. Existen resultados cuantitativos en esta transición de fase entre el flujo lento y el rápido.
Complejidad organizada versus pureza vacía
La arquitectura y la planeación urbana pueden ser entendidas como un proceso que incrementa el grado de complejidad organizada. Se ha escrito mucho acerca de la organización de la complejidad, especialmente desde el punto de vista biológico (Kauffman, 1995; Simon, 1962). La complejidad se genera cuando ocurren diferentes procesos al mismo tiempo; y si están organizados coherentemente, dan como resultado una complejidad organizada (Weaver, 1948). Cuando ocurren pocos procesos, la situación no es suficientemente compleja para empezar. Si por otro lado, existe complejidad pero está desorganizada, nos enfrentamos a una situación caótica. Esta situación es incomprensible para la mente humana, porque va más allá de nuestras habilidades perceptivas (Simon, 1962).
La humanidad se ha esforzado siempre por incrementar la complejidad organizada de su entorno, al mismo tiempo que desarrolla su inteligencia y mejora su comprensión de los sistemas naturales. Este siglo ha sido testigo de un retroceso deliberado en este proceso. Los arquitectos y planeadores urbanos se han encaprichado con la simplicidad visual y han ignorado el proceso fundamental de organización, que no es visualmente simple. Ahora contamos con muchos ejemplos de regiones urbanas en donde la complejidad ha sido eliminada a través de la supresión de conexiones (Batty y Longley, 1994). La búsqueda de pureza visual en un plano ha coartado seriamente las actividades humanas que fueron las que condujeron inicialmente a la urbanización (figura 4).
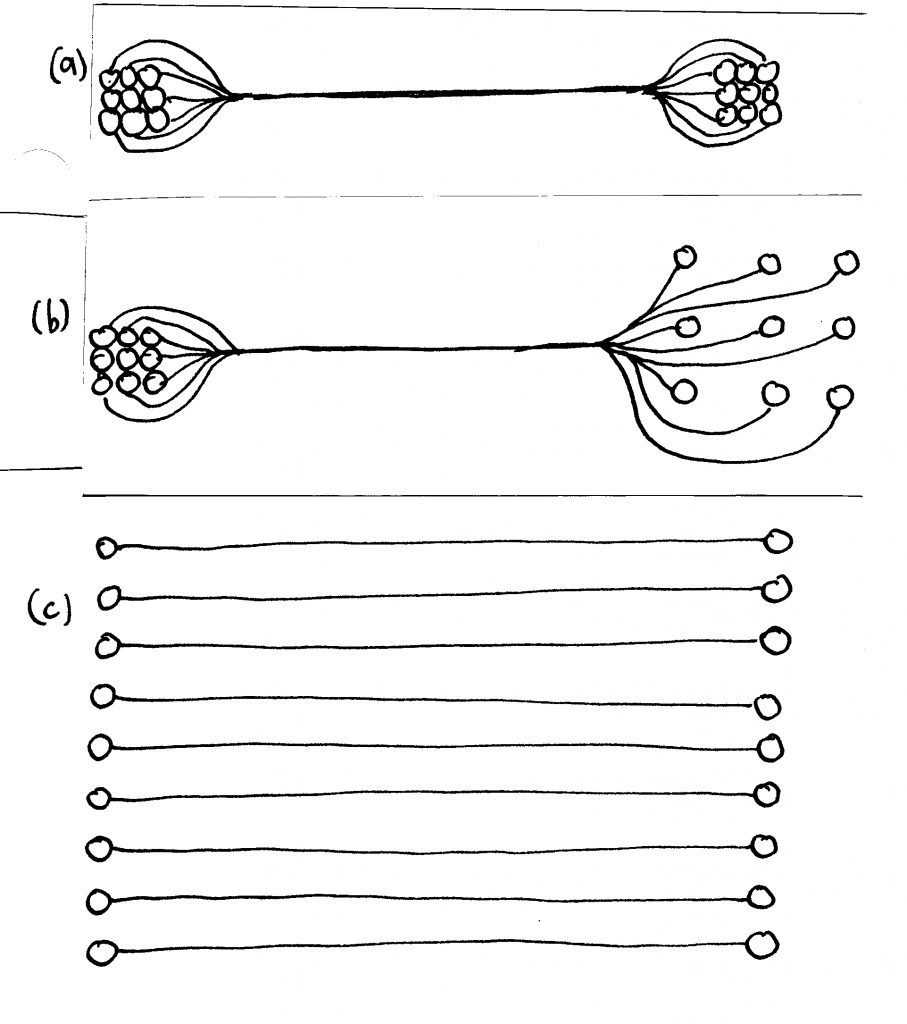
El modelo principal de planeación del siglo XX, la Ville Radieuse, no da lugar a las conexiones que forman la red urbana. Ese modelo sólo permite conexiones en pares entre la casa y el trabajo, no más (ver figura 4). Lo que tenemos es un paquete singular de pares de nodos conectados pero que no interactúan. Esto puede aplicarse también entre conjuntos de edificios de oficinas y de edificios de departamentos, y entre fábricas y casas suburbanas: el patrón está desconectado. El número de conexiones por pares es igual a N/2, que es el umbral antes de que empiecen a surgir las conexiones internas, explicado anteriormente en el “modelo de juguete”. Un gráfico completamente conectado necesita la mayor cantidad de conexiones (N – 1)N/2. El acoplamiento necesario para sostener la vida humana y sus actividades es ignorado deliberadamente en la Ville Radieuse.
Kevin Lynch introdujo la imagen mental de una ciudad como medio para juzgar su éxito (Lynch, 1960). Bill Hillier enfatizó la inteligibilidad de una ciudad como la facilidad con la cuál uno percibe la estructura de todas las trayectorias (Hillier, 1996). Aquí se puede precisar la conexión crucial entre la organización jerárquica y la simplificación. Un proceso caótico es simplificado por la organización sin que pierda necesariamente algo de su contenido intrínseco. Los elementos complejos y diversos se agrupan juntos de forma que cooperen y, como resultado, formen un todo. En contraste, la purificación es un proceso reductor que pierde mucha de la información inherente a un sistema. Desafortunadamente es muy fácil confundir ambos procesos, con consecuencias catastróficas.
Ahora sabemos mucho más sobre los procesos perceptivos que traza la trama urbana en la mente humana. Los dos son muy semejantes, y consisten en la interacción de redes de conectividad en diversos niveles. Una idea o una trayectoria, se establecen por la unión de filamentos cercanos de una red. La necesidad de tener muchas alternativas de trayectorias, y de compararlas, es la clave del pensamiento razonado. Un planificador puede forzar todo movimiento en una trayectoria única, pero esa no es la forma de trabajar de nuestras mentes; esa es la forma de trabajar de un robot (Fischler y Firschein, 1987). La búsqueda de inteligencia artificial en las máquinas corresponde precisamente al intento de moverse de la simplicidad vacía hacia la complejidad organizada.
El grado de organización de muchos sistemas complejos depende directamente del cociente del número de conexiones entre el número de nodos. La siguiente comparación es instructiva. En las computadoras digitales convencionales, el número de conexiones es comparable al número de nodos (transistores), lo que es aproximadamente lo que encontramos en una gráfica mínimamente conectada. En el cerebro, sin embargo, el número de conexiones es casi cuatro órdenes de magnitud más (i.e., 10,000 veces) más grande que el número de nodos (células nerviosas). Las computadoras neuronales múltiplemente conectadas, que son exitosas en el reconocimiento de patrones, están localizadas en algún número en medio. La analogía mente-red revela lo enorme que debe ser la densidad de las conexiones en un tejido urbano exitoso.
Algunas aplicaciones de la teoría
El resto de este escrito discute situaciones prácticas. Los tres principios dan lugar a algunas reglas que sugieren nuevas técnicas para construir mejores colonias. Estas reglas son aplicables a la planeación urbana en todas las escalas. Existen medidas que se pueden tomar para regenerar vecindades existentes. Se puede mejorar el funcionamiento de una región de forma drástica, alterando y aumentando sus conexiones. Los trabajos de Alexander y sus colaboradores, (Alexander, 1998; Alexander, Ishikawa, et al., 1977; Alexander, Neis et al., 1987), Gehl (1987), y Greenberg (1995), describen detalles bastante completos de soluciones específicas. El soporte teórico se deriva de los resultados de investigación de Batty (Batty y Longley, 1994) y de Hillier (Hillier, 1996; Hillier y Hanson, 1984), y sus colaboradores. En la parte siguiente de este capítulo se demuestra cómo las soluciones siguen a la discusión teórica.
Las trayectorias conectan nodos complementarios
Algunos planeadores urbanos bien intencionados incluyeron sendas peatonales en su diseño pero éstas no fueron utilizadas en la práctica. Entonces concluyeron que las personas ya no querían caminar, y en la siguiente oportunidad que tuvieron de construir, eliminaron estas sendas que entonces juzgaban como irrelevantes. Sin embargo, al rededor de todo el mundo, en ciudades y suburbios históricos, y en regiones que no han sido destruidas por la planeación insensible, la gente prefiere caminar, no solo por recreación y ejercicio, sino por rutina diaria. Increíblemente, los planeadores han olvidado el concepto básico de locomoción humana, y la han frustrado con estructuras construidas.
He planteado hasta el momento las razones por que las trayectorias prediseñadas son raramente funcionales. En primer lugar, por el proceso conectivo en sí mismo: en general, las conexiones ocurrirán solamente entre nodos contrastantes o complementarios. Esto surge de una ley básica de arquitectura (Salingaros, 1995), que descansa en sí misma sobre procesos físicos (figura 5). El flujo eléctrico ocurre solamente entre puntos con diferente potencial. La red urbana se crea por la necesidad de moverse a la escuela, a la casa, a un almacén comercial, a una oficina o a un parque; hay mucho menos necesidad de ir de una casa a otra. Los amigos “más cercanos” generalmente residen en otras colonias y no son los vecinos inmediatos.
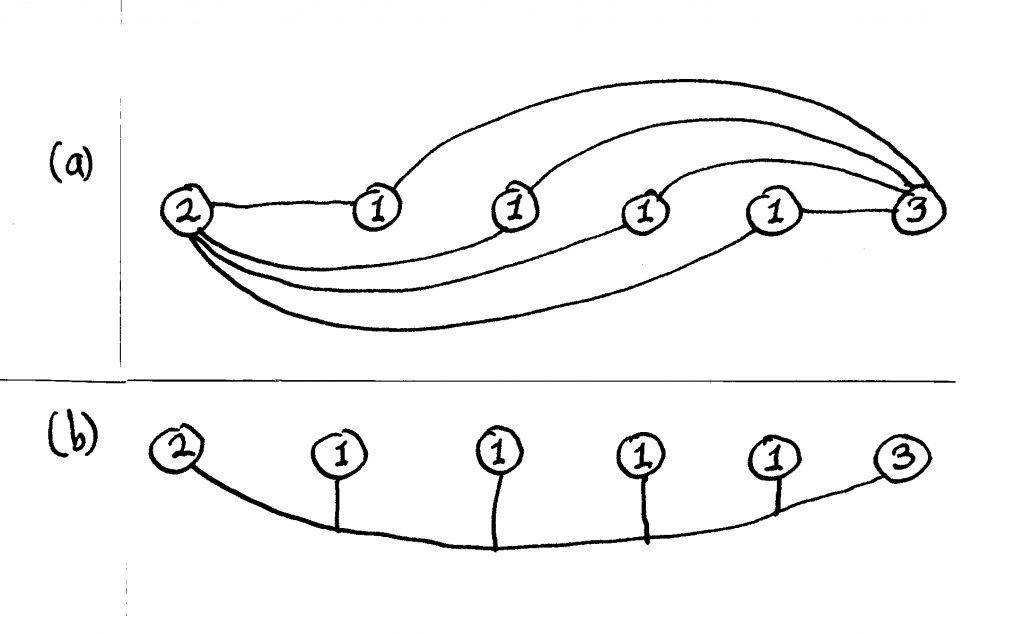
Las colonias funcionan solo si los nodos contrastantes están colocados de tal forma que propicien uniones activas entre nodos similares (ver figura 5). Esta es la clave para construir la red urbana: se establecen conexiones múltiples entre nodos complementarios, entonces se agrupan en trayectorias que también conectan nodos iguales. En contraste, las conexiones solo entre nodos iguales son demasiado débiles para conformar una trayectoria. Esta es la razón principal por la que los suburbios están muertos. Se necesita un balance entre nodos iguales y opuestos. En la conjunción de conexiones múltiples en una trayectoria, es importante que el canal no se sobrecargue, pero esto solo se atiende en situaciones de alta densidad (ver figuras 2 y 4).
Sin la suficiente densidad y variedad de nodos, las trayectorias funcionales (contrarias a las subutilizadas y puramente decorativas) no son posibles. Aquí se establece una posición en contra de la segregación y concentración de funciones que han destruido la red urbana en nuestros tiempos (ver figura 4). Simplemente no existe un número de nodos distintos en una región urbana homogénea que sea suficiente para formar una red. Aunque tenga posibilidades de existir, las conexiones son casi siempre bloqueadas por las mal dirigidas leyes de zonificación. Los distintos tipos de elementos, como residenciales, comerciales y naturales, deben interactuar para catalizar el proceso de conectividad (Alexander, Ishikawa et al., 1977). Las ciudades disfuncionales concentran nodos del mismo tipo, mientras que las ciudades funcionales concentran pares acoplados de nodos complementarios.
Paradójicamente, las conexiones que se dan entre nodos complementarios son el principio en el que se basa y opera la planeación urbana modernista. Sin embargo, este principio ha sido totalmente mal aplicado por los planeadores actuales que piensan estrictamente en las trayectorias del automóvil e ignoran las que son mucho más importantes: las conexiones peatonales. El ordenamiento jerárquico de distintos tipos de trayectorias es crucial para crear una red de conexiones, y será analizado en las próximas secciones. Analizando la importancia de las trayectorias cortas contra las largas, las demás conexiones de la red urbana — aquellas que no involucran al automóvil — deben ser violadas en los desarrollos suburbanos modernos. Esto incluye la relación auto-peatón.
Escalas humanas y conexiones en tramos
Los peatones requieren cierto rango limitado de escalas, fuera de las cuales no pueden funcionar (Gehl, 1987). Por ejemplo, la gente no quiere caminar más allá de una distancia máxima entre nodos (que puede ser determinada empíricamente). Esto significa que todas las trayectorias peatonales útiles están conectadas por tramos: son continuas pero no lineales (figura 6). Las grandes plazas fracasan porque normalmente incluyen sendas peatonales muy largas; en la mayoría de los casos, esas sendas están expuestas o pobremente definidas, lo que las hace menos funcionales aún. Los suburbios en general carecen de suficientes trayectorias de distancia corta entre nodos que alcancen para formar una red.
Un resultado matemático establece la forma de los segmentos individuales de una trayectoria: la distancia más corta entre dos puntos es una línea recta. Entonces, los peatones pueden ir de un nodo a otro a través de la línea lo más recta posible, evitando las esquinas, escaleras y cambios de nivel (Gehl, 1987). Este resultado sólo puede aplicarse en la escala más pequeña. Como se ha discutido anteriormente, existe una necesidad de tener trayectorias múltiples curvas o irregulares en las escalas mayores. Esto no es una contradicción, porque las dos están relacionadas en otro resultado matemático: cualquier curva global es una recta en el límite de su menor medida, es decir, una curva está formada por tramos rectos.
Todo el proceso de planeación comienza definiendo una conexión peatonal apropiada entre dos nodos de actividad. Si estas actividades están muy lejos una de la otra necesitamos introducir nodos adicionales a distancias intermedias, de otro modo, esta conexión no funcionará (ver figura 6). Los nodos necesitan estar conectados: esto crea trayectorias, sobre las cuales se crea la necesidad de otros nodos, requiriendo nuevas trayectorias, etc. De esta forma, la red urbana se genera a sí misma. Mientras más coherente sea la subestructura, la red es más estable.
Jerarquía y fractales
Si observamos desde el aire a una ciudad que funciona, la imagen es obviamente la de un fractal (Batty y Longley, 1994). Esto no es solo una coincidencia visual; Michael Batty y su grupo de colaboradores han desarrollado rigurosamente la esencia natural fractal de la red urbana (Batty y Xie, 1996). En contraste, la imagen de una ciudad artificial, muerta, es mucho más regular en planta y no tiene una estructura a menor escala. Lo que vemos en el primer caso es una jerarquía de redes, todas interrelacionadas y en diferentes escalas, desde una vía rápida hasta una senda peatonal. La estructura de menor escala es lo que eventualmente garantiza la vitalidad humana de una ciudad; las conexiones en la gran escala solo facilitan el movimiento a mayor escala.
Hillier y sus colaboradores (Hillier, 1996; Hillier y Hanson, 1984) han probado simulaciones por computadora de la forma en que la ciudad se genera. Entre muchos de los resultados obtenidos que son relevantes a nuestro tema, surge uno abrumador: la estructura espacial de las ciudades es el resultado desordenado de una larga historia de incrementos en los cambios de menor escala. Los patrones resultantes no son simples ni en geometría ni en función. El diseño de un objeto global — la ciudad — surge en sí misma de acuerdo con un sistema localmente ordenado. Estos resultados no se analizarán en este escrito pues ellos marcan la importancia de comenzar con la escala más pequeña y permitir su evolución para que influencien las escalas mayores.
El éxito de las áreas de comercios pequeños y las plazas
Mike Greenberg, un agudo observador de situaciones urbanas, analiza el rol que juegan las conexiones en el éxito de las áreas de pequeños comercios (Greenberg, 1995). Las características de las sendas peatonales establecen una longitud máxima pero no una mínima para cada segmento. Mientras más segmentada esté la trayectoria (en virtud de tener más nodos intermedios) más fuerte y firme será la estructura de la red. Las calles antiguas de comercios contienen nodos (tiendas) una al lado de la otra. La variedad y proximidad de las tiendas les permite estar ligadas a un distrito comercial. Los centros comerciales grandes van un paso más allá y también incluyen conexiones pequeñas entre los frentes opuestos de las tiendas, que generalmente no es posible en una ciudad porque los frentes de las tiendas están separadas por una vía vehicular (Greenberg, 1995) (Figura 7).
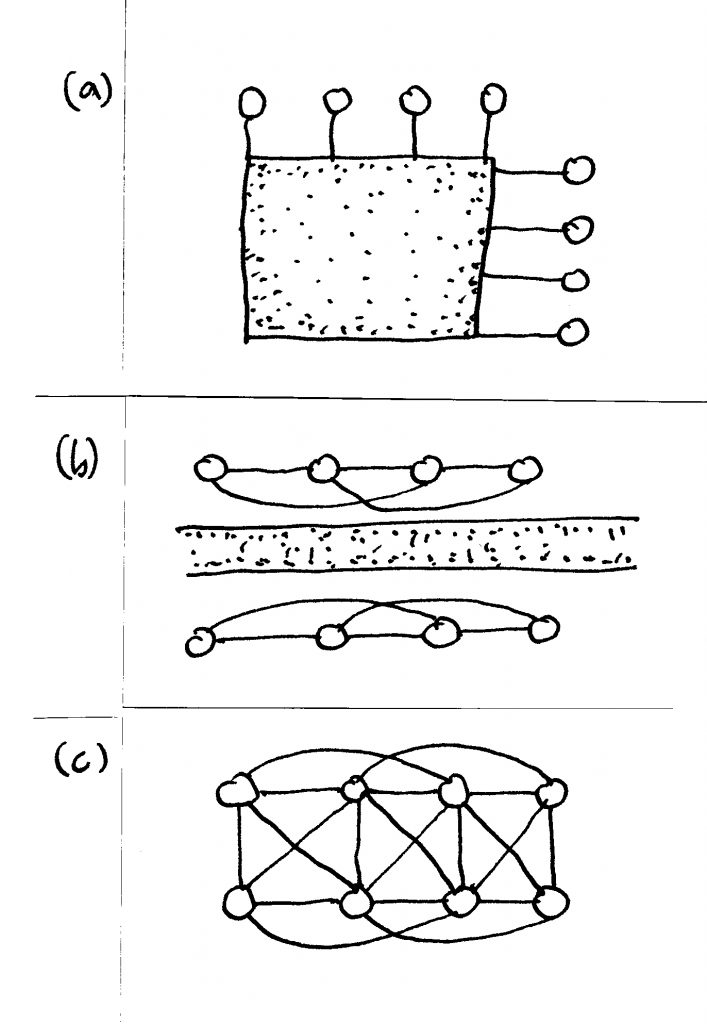
La misma solución se aplica a una plaza bien planeada. Una zona peatonal no se crea por la simple prohibición del tráfico vehicular; está definida por el traslape y entrecruzamiento de trayectorias peatonales. La peatonalización es recomendable si es imposible definirla con solo una o dos trayectorias que ordenen las conexiones peatonales. Según lo discutido anteriormente, las distintas trayectorias deben conectar puntos de interés complementarios. Una plaza que funciona se define por contener tipos opuestos de nodos en todo su alrededor. Si no existe tráfico que les impida caminar a los peatones y si es posible que las trayectorias cubran casi toda el área, entonces es mejor convertirla en una zona peatonal en vez de crear muchas trayectorias separadas.
Una trayectoria como el borde de una región
Las trayectorias son elementos matemáticos lineares definidos por la diferenciación entre regiones contrastantes o distintas. Una trayectoria que atraviesa un área uniforme, es ambigua, porque divide al área en componentes similares en ambos lados; ésta puede ser colocada donde sea dentro de ese área. (Es importante notar que una multiplicidad de trayectorias bien definidas es el opuesto de una sola trayectoria ambigua). Una trayectoria funciona solo si coincide con el límite de un área, como el borde de un edificio (Gehl, 1987), así se combina de forma esencial con dos elementos urbanos de Lynch: trayectorias y bordes (Lynch, 1960) (figura 8). En ausencia de un borde existente, un muro crea una división a lo largo de la cuál se puede desarrollar una trayectoria. Mientras que Lynch denota que algunas veces las trayectorias se desarrollan a lo largo de los bordes, debemos insistir en que las trayectorias y los bordes son potencialmente una unidad. En la teoría de las gráficas, en lo que se propone como significado para el entendimiento de la red urbana, las trayectorias y los bordes son lo mismo.
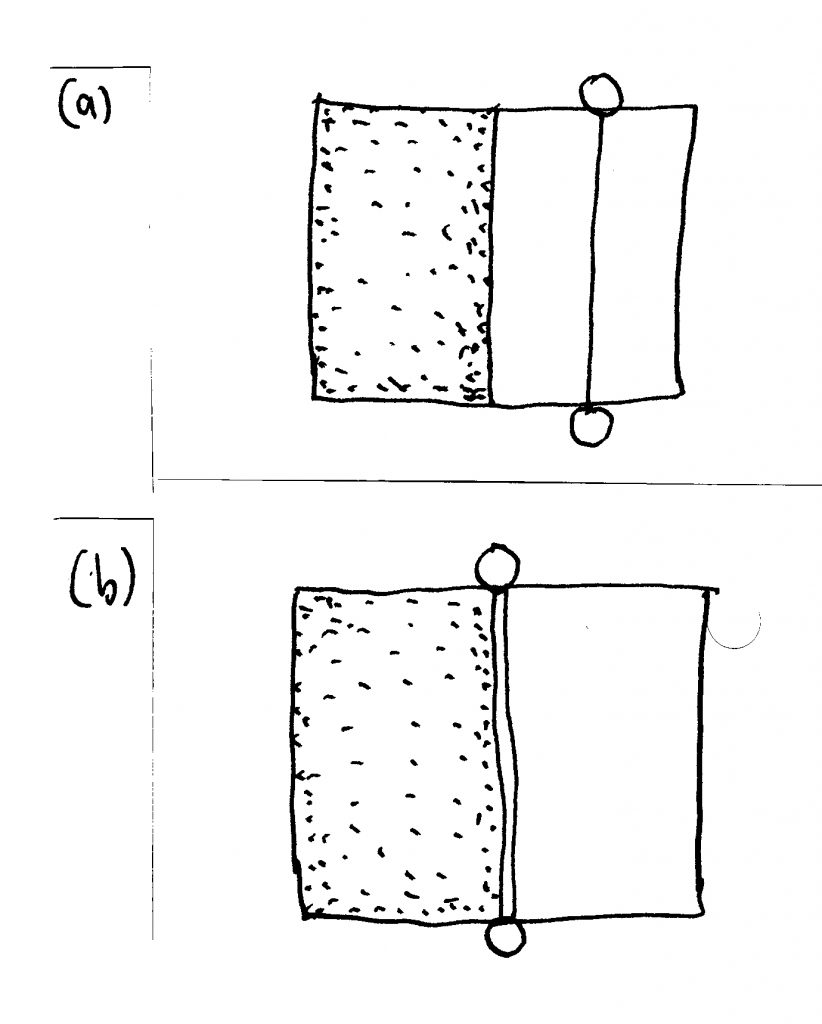
Para lograr máxima estabilidad se requiere que cada elemento de la red urbana refuerce a todos y cada uno de los otros elementos. Si no, las fuerzas que se generan desequilibran o interrumpen el diseño. Desde el punto de vista de la división de un área, una trayectoria modifica a la unidad original de ese área; es una intrusión, por lo tanto el área no la refuerza. Es muy diferente cuando se crea una trayectoria a lo largo de un borde entre dos áreas distintas. La trayectoria ahora apoya al borde y viceversa. Una ley en arquitectura define a las unidades por contraste (Salingaros, 1995): cualquier división debe realizarse dentro de un par complementario, no dentro de un par similar.
Existen datos psicológicos que refuerzan esta propiedad de las trayectorias. La gente no se siente cómoda caminando en medio de los espacios, con el mismo ambiente (o abierto y desprotegido; o sumamente encerrado) en ambos lados (Gehl, 1987). Esto es una expresión de sensaciones del subconsciente para protegerse del peligro; uno quiere estar cerca de algo sólido, dando el frente hacia afuera. Las trayectorias necesitan ser protegidas por un borde. Esta es la razón por la cuál una cerca no substituye a un muro, y por la que las grandes planchas de estacionamiento son tan deshumanizante. El otro extremo, en donde una trayectoria está encerrada entre muros en ambos lados, es claustrofóbico. Una plaza funciona mejor si proporciona un borde sustancial que rodee sus múltiples trayectorias.
Prioridad en la creación de trayectorias peatonales
La red urbana está formada por redes de conexiones traslapadas. No hay razón para suponer, como muchos planeadores lo hacen, que las diferentes redes deben coincidir. Existen diferentes tipos de conexiones en las diferentes escalas, por lo tanto, matemáticamente no pueden coincidir. La red tiene fuerza estructural sólo cuando las redes de los distintos niveles se crucen y traslapen, propiciando la conectividad cruzada. Cuando las conexiones son forzadas a coincidir se vuelven singulares (muchas conexiones se concentran a lo largo de una trayectoria). Las conexiones singulares no funcionan porque sobrecargan la capacidad del canal (ver figuras 2 y 4).
El número de trayectorias peatonales en la red urbana debe ser mucho mayor al que existe hoy. Una tendencia desafortunada de los últimos 70 años ha sido la de limitar las sendas peatonales por la imposición arbitraria de una retícula rectangular (o otra retícula restrictiva) para todas las conexiones (Batty y Longley, 1994). El segundo error ha sido el de dar prioridad a las sendas vehiculares sobre las sendas peatonales. Alexander y asociados observaron el proceso del establecimiento de conexiones en las redes (Alexander, Neis et al., 1987). Concluyeron que existe una secuencia óptima que puede seguirse: definir primero el espacio peatonal y verde, seguido por las conexiones peatonales, edificios y caminos, en ese orden (Alexander, Neis et al., 1987). Las mejores ciudades del pasado fueron construidas siguiendo esta secuencia. Un estudio cuidadoso de la red urbana muestra claramente que si se sigue el orden inverso, como se hace en estos días, se elimina a las áreas peatonales y a las áreas verdes realmente utilizables.
Los nodos de un barrio deben estar conectados mediante sendas peatonales funcionales. En nuestros días esto ocurre sólo en algunos barrios antiguos (anteriores a 1940). Los conjuntos de casas deben estar conectados también por ciclopistas. Esto no significa necesariamente la variedad de pavimento separado dedicado a la ciclopista, sino hacer un camino confiable para andar en bicicleta sin la necesidad de bajarse de ella o con el constante peligro que existe para un ciclista en una calle transitada. (Este concepto se debe a Greenberg (1995)). Cuando los conjuntos de casas están conectados solo por una calle local, las conexiones peatonales y de bicicletas se descuidan. En la mayoría de los casos, por otra parte, esta calle no es estrictamente local sino una avenida de doble sentido muy transitada, lo que hace que la situación sea peor.
Las sendas peatonales no tienen que estar estrictamente distintas y separadas de las ciclopistas. Tampoco necesariamente distintas o separadas de las calles; todo depende de la densidad del tráfico. De hecho, los peatones anhelan la conexión visual que proporciona una senda peatonal a lo largo de una calle. Esto incrementa los requerimientos de seguridad, pues las sendas peatonales desoladas son peligrosas. Mientras que el flujo vehicular no sea tanto que resulte incómodo, una senda peatonal puede correr paralelamente y al lado de una calle. Las sendas peatonales pueden también coincidir con avenidas si se toman las medidas apropiadas para disminuir la velocidad vehicular (Gehl, 1987).
Garantizar la funcionalidad de las trayectorias individuales
Las partes anteriores de este capítulo hablan sobre establecer la mayoría de trayectorias posibles para conectar los nodos dentro de la red urbana. Sin embargo, hay un límite para este proceso. Como en todos los sistemas naturales conectados, sólo deben establecerse aquellas conexiones que funcionen; aquellas que sean verdaderamente necesarias para la conectividad múltiple. Existen algunas pautas que ayudan al juzgar cuando una conexión va a ser utilizada y cuándo no. Se recomienda evitar las conexiones que, por cualquier razón, no sean utilizadas, incluyendo debido a los factores que no se han discutido aquí. Por ejemplo, haciendo más pequeño el tamaño de las cuadras — una solución urbana comúnmente propuesta — no siempre garantiza que las calles recién creadas serán utilizadas por el tráfico suficiente. Es necesario justificar el costo adicional de su construcción y ofrecer seguridad contra el crimen (Hillier y Hanson, 1984).
En otra situación, cuando una ciudad lucha por el derecho de vía a través de un lote comercial, esta trayectoria debe ser utilizada, de otro modo, el proceso se desacredita para futuras aplicaciones. El diseñador urbano debe optimizar las condiciones para que una trayectoria tenga suficiente tráfico para hacerla viable. Las no-trayectorias disfuncionales son producto del pensamiento en términos de regularidad geométrica; con esta forma de pensar, las trayectorias se conciben (equivocadamente) como una clase de simetría visual dentro del plan. Aunque el modelo actual de la red urbana nos libera de este error en teoría, existe sólo un pequeño límite que distingue una trayectoria funcional de una que no funciona, y esto no se observa obvio en un plano. Tampoco son evidentes muchos de los factores que influencian el éxito de una trayectoria.
Algunas personas inteligentes y perceptivas afirman que la ciudad peatonal está muerta, y sólo podría existir bajo condiciones que ya no pueden reproducirse. No estoy de acuerdo. El motivo de su pesimismo es que parece que las sendas peatonales ya no funcionan. Yo afirmo que muchas trayectorias actuales son artificiales, decorativas, que no pueden ser forzadas a funcionar. Éstas corresponden a una línea incorrecta en un bosquejo. Para reparar las regiones urbanas existentes, necesitamos borrar esas líneas equivocadas; es decir, se eliminan o transportan las trayectorias que son inútiles y de tipo frustrante. Si no pueden ser arregladas, las no-trayectorias existentes aíslan al edificio de una trayectoria funcional cercana, lo que representa un impedimento para generar el tejido urbano. En muchas regiones, tales no-trayectorias han sustituido a las trayectorias útiles de tipo antiguo, estableciendo así un patrón dañado que copiarán los planeadores urbanos.
El patrón de las calles como principio de organización
El tránsito vehicular está diseñado para facilitar la actividad humana. Después de que se establezcan los elementos naturales, los arquitectónicos y las conexiones peatonales, se pueden introducir las calles para organizar las conexiones dentro de una escala mayor (Alexander, Neis et al., 1987; Greenberg, 1995) (Figura 9). Es esencial establecer calles vehiculares en la jerarquía apropiada. En cualquier sistema complejo, la organización debe establecerse desde la escala pequeña hacia la grande. Cada tipo de calle sirve diferentes densidades de tráfico, y un solo tamaño no puede satisfacer las necesidades de todo. Muchas redes de conexión independientes tendrán que intersectarse en puntos diferentes. Cada tipo de intersección presenta un problema especial a resolver, de otro modo, la circulación sería interrumpida (Alexander, Ishikawa et al., 1977; Greenberg, 1995). (Los puntos de cruce no se analizan en este escrito).
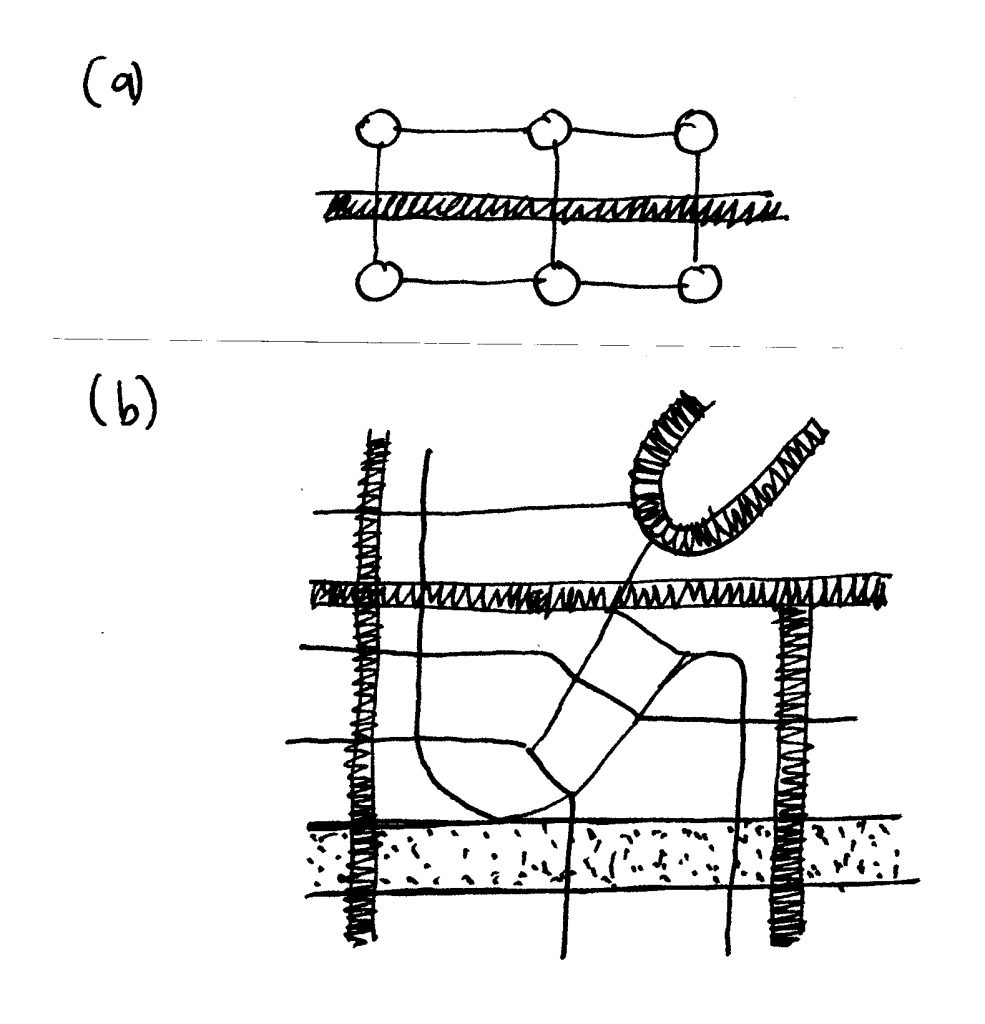
Existe hoy una gran cantidad de calles vehiculares de media densidad que tratan de satisfacer (con efectividad limitada) a muy distintos flujos de tráfico. Las calles curvas y sin salida evitan el tráfico en las nuevas subdivisiones suburbanas. Sin embargo, su aplicación es paradójica, porque tratan de reducir el flujo vehicular mientras su constitución en anchura y materiales son características de una avenida de alta velocidad (Gehl, 1987). Esto ignora y corta las sendas peatonales y ciclopistas, que podrían cruzar efectivamente sólo una calle de poca capacidad de flujo. También, la red de conexiones debe continuar en todas direcciones, para que en cualquier lugar que se termine una cale, las sendas peatonales y la gente en bicicleta pueda continuar su camino sobre una trayectoria entre las casas. Las sendas peatonales y ciclopistas deben constituir redes totalmente independientes de los caminos locales (Alexander, Ishikawa et al., 1977) (ver figura 9).
En este punto se llega a una observación crucial de los sistemas complejos: la organización jerárquica requiere que los componentes de distintos tamaños encajen perfectamente en el todo. Las piezas de la red urbana son simples, e interactúan de forma sencilla; aunque su unión es muy compleja. El método para colocarlas juntas debe respetar esta complejidad (Alexander, 1964; 1965). No se pueden resolver los problemas que son inherentes al proceso organizacional sobre un papel ni en un día. Los sistemas jerárquicos dependen de la interacción adecuada de los elementos conectados en muchos y distintos niveles, y requieren necesariamente un proceso dinámico para su crecimiento. Cualquier intento simplista de organización está limitado por faltar las conexiones que contribuyan a la estabilidad interna.
En el presente modelo no se ha desarrollado en el tema de cómo la dinámica entre calles y sendas se relaciona con el funcionamiento de las ciudades. El lógico interno de la retícula desordenada de una ciudad se basa fundamentalmente en el movimiento, para que muchas de las propiedades del espacio urbano sean producto de sus conexiones (Hillier, 1996; Hillier y Hanson, 1984). Una fuente de literatura sobre space syntax — empezando por el trabajo de Hillier y sus colaboradores (Hillier, 1996; Hillier y Hanson, 1984) — es el periódico Environment and Planning B. Ese trabajo trata de asociar las redes peatonales y las redes de las calles con el crimen y la congestión, especialmente en los estados habitacionales. En este contexto, los encargados de modelar el tráfico, asignan tráfico de muchos orígenes y destinos a una cantidad reducida de trayectorias, espejeando las figuras 2 y 4. Esta simplificación de la retícula urbana de calles exacerba los problemas específicos que se tratan de resolver.
Son necesarias las discontinuidades y la separación
No todos los nodos de la red deben estar conectados unos con otros. Tomando como referencia a los sistemas biológicos, los diferentes órganos podrían interferir entre sus funciones a menos que estén separados localmente. Existen elementos en la red urbana que se pueden dañar unos a otros a menos que se tenga cuidado de aislarlos. Algunos ejemplos son: una avenida de alta velocidad al lado de un complejo habitacional, una senda peatonal al lado de una avenida, industria pesada al lado de casas, un tugurio cerca de una zona residencial de nivel alto (figura 10). Todos estos son componentes necesarios de una ciudad, y usualmente están aislados unos de otros por alguna clase de barrera (Alexander, Ishikawa et al., 1977). Esto no es un enunciado sociológico, es sólo una observación de lo que realmente sucede. Lynch (1960) enfatizó el rol importante y necesario que juega un borde como un límite.
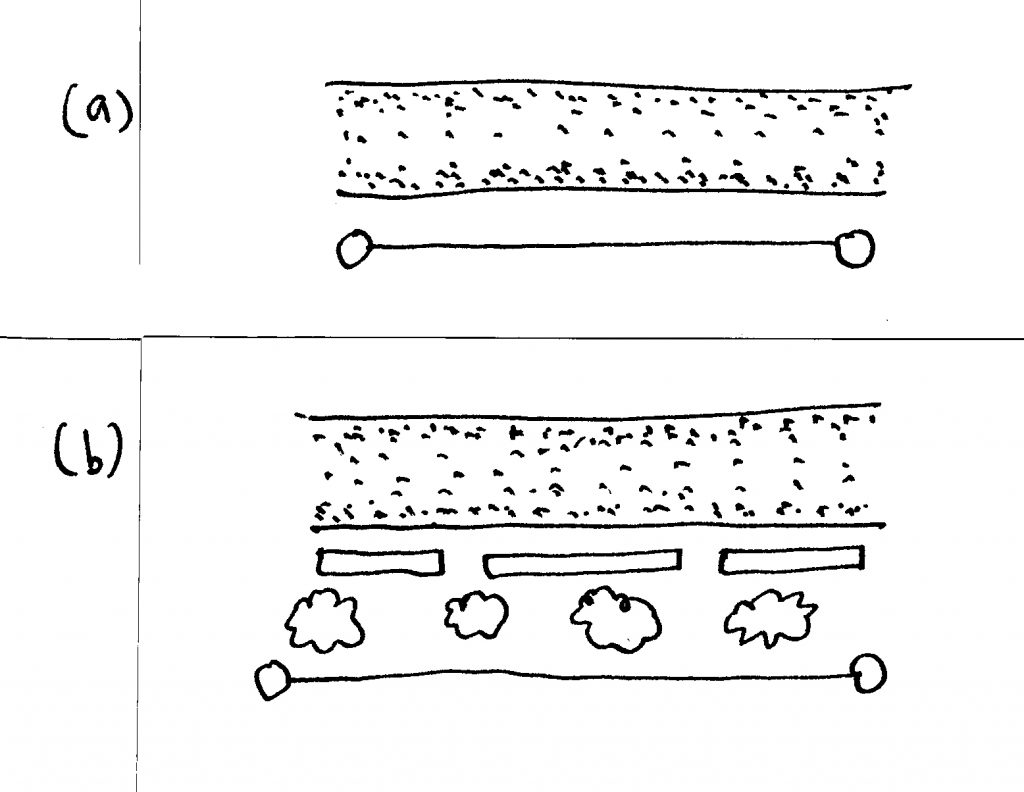
Una banqueta colindante con una avenida de alta velocidad es peligrosa, y por lo tanto, es raramente utilizada. Sobrevive como un remanente anacrónico de las pequeñas ciudades con tráfico de baja velocidad. Últimamente no se ha pensado en la interacción entre peatones y autos. En esta situación, una banqueta debe estar aislada por una barrera: ya sean secciones de un muro sólido, o una amplia área verde con árboles (ver figura 10). No hay necesidad de conexión (a excepción de la visual) entre peatones y tráfico de alta velocidad. Cualquier calle en la que un auto no pueda pararse para recoger o descargar pasajeros está efectivamente aislada, y debe estar designada de ese modo.
Las funciones urbanas dispares y las vecindades tienden a coexistir en un equilibrio más sano cuando están separadas por una barrera (Alexander, Ishikawa et al., 1977). No se habla de separar las áreas comerciales de las residenciales, que tienen que interactuar, pero sí el uso de bordes como límites constructivos. Las calles de alta densidad cortan con eficacia al tejido urbano. Otras soluciones incluyen una pared, un río o un gran parque; todos estos elementos se encuentran en las viejas ciudades. En las nuevas urbanizaciones, los ríos son excedentes de la ciudad y son cubiertos porque no encajan en la retícula rectangular, y se pierde así una excelente barrera natural. A menudo, una barrera existente ha conducido al crecimiento diferenciado de las áreas en sus lados. En otros casos, un límite ha proporcionado estabilidad a largo plazo en una colonia.
Se mencionan los límites porque ahora son colocados en los lugares equivocados. Matemáticamente, todavía tenemos solo nodos de red y conexiones. Como se mencionó anteriormente, los muros son ideales para reforzar las trayectorias y los caminos, pero en vez de eso ahora son utilizados para bloquear conexiones. Una barda sólida necesita aberturas que permitan a las trayectorias pasar a través de ella. Los elementos conectivos fuertes, como avenidas, necesitan ser introducidas a la ciudad en algún punto. En vez de ser colocadas donde realmente se necesita una separación, se colocan invariablemente de forma que atraviesan muchas conexiones existentes. Los elementos de conexión y de aislamiento son complementarios, y su mala aplicación para un objetivo opuesto se basa en el mal entendimiento de la red urbana.
El crimen local puede destruir también las conexiones en las vecindades que, hasta este punto, han estado trabajando bastante bien. Cuando el tejido urbano es amenazado, reacciona orgánicamente construyendo cercas para protegerse, en analogía a un tejido de cicatrización que se ensancha sobre la cicatriz de una herida biológica. Este acto singular reorganiza un espacio, separando las conexiones que provocan que sea una fuente de crimen. Si esa fuente no se localiza, cada nodo o grupo de nodos se aislará con una cerca, rasgando el tejido urbano. Una vecindad puede recuperarse del crimen local, pero el tejido urbano nunca puede recuperarse una vez que se bloquean las conexiones.
Conclusión
Este capítulo derivó una serie de principios de planeación de consideraciones matemáticas, sumadas al proceso conectivo que genera a la red urbana. Los principios se cumplen en todos los ambientes urbanos exitosos alrededor del mundo. Por otro lado, son violados en los ambientes urbanos que fallan, que no son amigables, que no son satisfactorios, que están aislados y que están deshumanizados. Con la aplicación de las leyes de zonificación que violan las necesidades conectivas, somos responsables de muchas de esas fallas. Sin embargo, es posible crear nuestras ciudades de acuerdo a los principios matemáticos apropiados que están detrás de las actividades humanas.
El mantenimiento de una gran variedad de trayectorias y espacios verdes es inevitablemente costoso. Todas las indicaciones, sin embargo, se refieren a que el costo para la sociedad es incomparablemente mayor si no se implementan estas soluciones. La interrupción de un barrio lleva a la alienación e incremento del crimen; seguido por la huida a los suburbios y el decremento del sentido de pertenencia (y el valor inmobiliario). En términos financieros, el resultado final del intento por ahorrar en la cuenta para alcanzar un balance adecuado de elementos urbanos podría terminar en la pérdida de la mayor parte de las áreas que recaudan ingresos fiscales. En términos humanos, el resultado puede ser devastador. Estos últimos costos deben ser cuidadosamente considerados por los planeadores urbanos.
Reconocimientos.
El autor se ha beneficiado de muchas discusiones sostenidas con Mike Greenberg.
Primera publicación in Journal of Urban Design, volume 3, 1998, páginas 53-71.
Traducción: Nuria F. Hernández Amador
veredes, arquitectura y divulgación está colaborando con el autor para publicar algunos capítulos de su libro «Principles of Urban Structure« traducidos gratis en la red, para el beneficio de los estudiantes hispanohablantes en todo el mundo. El libro en versión inglesa está publicado en Holanda, los EEUU y Nepal.
Referencias.
Albert, R., Jeong, H-W. and Barabási, A-L. (1999) “Diameter of the World-Wide Web”, Nature, Vol. 401, pp. 130.
Alexander, C. (1964) Notes on the Synthesis of Form, Cambridge, Massachusetts: Harvard University Press.
Alexander, C. (1965) “A City is Not a Tree”, Architectural Forum, Vol. 122, No. 1, pp. 58-61 and No. 2, pp. 58-62. Translated into many languages. Reprinted in: Design After Modernism, Edited by J. Thackara, Thames and Hudson, London (1988), pp. 67-84. Published electronically by RUDI (2001): <http://www.patternlanguage.com/archives/alexander1.htm>. Versión Castellana: ¿
Alexander, C. (1979) The Timeless Way of Building, Oxford University Press, New York. El Modo Intemporal de Construir, Barcelona: Editorial Gustavo Gili, 1981.
Alexander, C. (2002) The Nature of Order, Berkeley, California: The Center for Environmental Structure.
Alexander, C., Ishikawa, S., Silverstein, M., Jacobson, M., Fiksdahl-King, I. and Angel, S. (1977) A Pattern Language, New York: Oxford University Press. Un Lenguaje de Patrones, Barcelona: Editorial Gustavo Gili, 1980.
Alexander, C., Neis, H., Anninou, A. and King, I. (1987) A New Theory of Urban Design, New York: Oxford University Press.
Alexander, C., Silverstein, M., Angel, S., Ishikawa, S. & Abrams, D. (1975) The Oregon Experiment, Oxford University Press, New York. Une Expérience d’Urbanisme Démocratique, Paris: Éditions Seuil, 1976.
Allegrini, P., Barbi, M., Grigollini, P. and West, B.J. (1995) “Dynamical Model for DNA Sequences” Physical Review E, Vol. 52, pp. 5281-5296.
Allen, P. M. (1997) Cities and Regions as Self-Organizing Systems: Models of Complexity, Amsterdam: Gordon and Breach.
Bacon, E. N. (1974) Design of Cities, Harmondsworth, Middlesex, England: Penguin Books.
Barabási, A. L. (2002) Linked: The New Science of Networks, , Cambridge, Massachusetts: Perseus Publishing.
Batty, M. and Xie, Y. (1996) “Preliminary Evidence for a Theory of the Fractal City”, Environment and Planning A, Vol. 28, pp. 1745-1762.
Batty, M. and Longley, P. (1994) Fractal Cities, London: Academic Press.
Bollobás, B. (1985) Random Graphs, London: Academic Press.
Bonner, J. T., (1988) The Evolution of Complexity by Means of Natural Selection, Princeton, New Jersey: Princeton University Press.
Booch, G. (1991) Object Oriented Design, Redwood City, California: Benjamin/Cummings.
Bovill, C. (1996) Fractal Geometry in Architecture and Design, Boston: Birkhäuser.
Brand, S. (1995) How Buildings Learn, New York: Penguin Books.
Buchanan, M. (2002) Nexus: Small-worlds and the Groundbreaking Science of Networks, New York: W. W. Norton & Company.
Calder, W. A., (1984) Size, Function and Life History, Cambridge, Massachusetts: Harvard University Press.
Castells, M. (1989) The Informational City, Oxford: Blackwell.
Charles Prince of Wales (1989) A Vision of Britain, London: Doubleday.
Collins, G. R. and Collins, C. C. (1986) City Planning According to Artistic Principles, by Camillo Sitte, New York: Random House. [Der Städte-Bau, Carl Graeser Verlag, Vienna, 1901]
Coplien, J. O. and Schmidt, D., Ed. (1995) Pattern Languages of Program Design, Reading, Massachusetts: Addison-Wesley.
Courtois, P.-J. (1985) “On Time and Space Decomposition of Complex Structures”, Communications of the ACM, Vol. 28, pp. 590-603.
Coward, L. A. (1990) Pattern Thinking, New York: Praeger.
Coward, L. A. (2000) “A Functional Architecture Approach to Neural Systems”, Systems Research and Information Systems, Vol. 9, pp. 69-120.
Coward, L. A. (2001) “The Recommendation Architecture: Lessons from Large-Scale Electronic Systems Applied to Cognition”, Journal of Cognitive Systems Research, Vol. 2, pp. 111-156.
Cullen, Gordon (1961) The Concise Townscape, Oxford: Butterworth.
Dovey, K. (1990) “The Pattern Language and its Enemies”, Design Studies, Vol. 11, pp. 3-9.
Drewe, P. (1999) “In Search of New Concepts of Physical and Virtual Space”. In: Proceedings of the Conference: “Cities in the Global Information Society: an International Perspective”, University of Newcastle, Newcastle-upon-Tyne, November 22-24. Published in: M. Schrenk (ed.), Beitrage zum 5. Symposion “Computergestützte Raumplanung”—CORP 2000, Volume 1, Vienna University of Technology, pp. 37-44.
Drewe, P. (2000) “ICT and Urban Form: Planning and Design Off the Beaten Track”, Delft University of Technology, Design Studio ‘The Network City’, Faculty of Architecture.
Droege, P. (ed.), (1997) Intelligent Environments, Amsterdam: Elsevier.
Dupuy, G. (1991) L’Urbanisme Des Réseaux, Paris: Armand Colin.
Dupuy, G. (1995) Les Territoires de l’Automobile, Paris: Anthropos.
Edelman, G. M. and Tononi, G. (2000) A Universe of Consciousness, New York: Basic Books.
Eilenberger, G. (1985) “Freedom, Science, and Aesthetics”, in: Frontiers of Chaos, edited by: H. O. Peitgen and P. H. Richter (Bremen, Germany, MAPART, Forschungsgruppe Komplexe Dynamik der Universität), pp. 29-36.
Elia, M. M. (1996) Louis Henry Sullivan, New York: Princeton Architectural Press.
Erickson, T. (2000) “Lingua Francae for Design: Sacred Places and Pattern Languages”, in: Proceedings of the ACM Conference on Designing Interactive Systems 2000, New York: ACM Press, pages 357-368. [Brooklyn, New York, August 17-19, 2000]
Fathy, H. (1973) Architecture for the Poor, Chicago: University of Chicago Press.
Fischler, M. A. and Firschein, O. (1987) Intelligence: The Eye, the Brain, and the Computer, Reading, Massachusetts: Addison-Wesley.
Frankhauser, P. (1994) La Fractalité des Structures Urbaines, Paris: Anthropos.
Friedman, A. (1997) “Design for Change: Flexible Planning Strategies for the 1990s and Beyond”, Journal of Urban Design, Vol. 2, pp. 277-295.
Gabriel, R. (1996) Patterns of Software. New York: Oxford University Press.
Gamma, E., Helm, R., Johnson, R. and Vlissides, J. (1995) Design Patterns, Reading, Massachusetts: Addison-Wesley.
Garlan, D., Allen, R. and Ockerbloom, J. (1995) “Architectural Mismatch, or Why it’s hard to build systems out of existing parts”. In: Proceedings of the Seventeenth International Conference on Software Engineering, IEEE Computer Society, New York: ACM Press, 179-185. Revised version in: IEEE Software, Vol. 12 (November 1995), pp. 17-26.
Garnsworthy, A. and O’Connor, K. (1997) “Knowledge-Based Manufacturing and Regional Change”, in: Intelligent Environments, edited by: P. Droege, Amsterdam: Elsevier, pp. 87-97.
Gehl, J. (1987) Life Between Buildings, New York: Van Nostrand Reinhold. [reprinted by Arkitektens Forlag, Copenhagen, Denmark, Fax 45 33912770]
Gleick, J. (1987) Chaos, New York: Viking/Penguin.
Graham, S. and Marvin, S. (1996) Telecommunications and the City, London: Routledge.
Graham, S. and Marvin, S. (2001) Splintering Urbanism, London: Routledge.
Greenberg, M. (1995) The Poetics of Cities, Columbus: Ohio State University Press.
Habraken, N. J. (1998) The Structure of the Ordinary, Cambridge, Massachusetts: MIT Press.
Hallowell, E. M. (1999) “The Human Moment at Work”, Harvard Business Review (January-February 1999), pp. 58-66.
Hanson, B. and Younés, S. (2001) “Reuniting Urban Form and Urban Process”, Journal of Urban Design, Vol. 6: pp. 185-209.
Hester, R. T. (1993) “Sacred Structures and Everyday Life: A Return to Manteo, North Carolina”, in: Dwelling, Seeing, and Designing, Edited by: David Seamon, New York: State University of New York Press, pp. 271-297.
Heylighen, F. (1999) “Collective Intelligence and its Implementation on the Web”, Computational and Mathematical Organization Theory, Vol. 5: pp. 253-280.
Highsmith, J. A. (2000) Adaptive Software Development, New York: Dorset House Publishing.
Hillier, W. R. G. and Hanson, J. (1984) The Social Logic of Space, Cambridge: Cambridge University Press.
Hillier, B. (1996) Space is the Machine, Cambridge: Cambridge University Press.
Hillier, B. (1997) “Cities as Movement Economies”, in: Intelligent Environments, Edited by: P. Droege, Amsterdam: Elsevier, pp. 295-342. Appears as Chapter 4 of: Bill Hillier (1996) Space is the Machine, Cambridge: Cambridge University Press.
Hillier, B. (1999) “The Hidden Geometry of Deformed Grids”, Environment and Planning B, Vol. 26, pp. 169-191.
Hillis, W. Daniel. (1992) “Co-Evolving Parasites Improve Simulated Evolution as an Optimization Procedure”. In: Artificial Life II, edited by C. G. Langton, C. Taylor, J. D. Farmer & S. Rasmussen, Reading, Massachusetts: Addison-Wesley, pp. 313-324.
Hillis, W. D. (1998) The Pattern on the Stone, New York: Basic Books.
Jacobs, J. (1961) The Death and Life of Great American Cities, New York: Vintage Books.
Johnson, S. (2001) Emergence, New York: Scribner.
Kauffman, S. (1995) At Home in the Universe, New York: Oxford University Press.
Kaye, B. H. (1994) A Random Walk Through Fractal Dimensions, 2nd Edition, Weinheim, Germany: VCH Verlagsgesellschaft.
Krier, L. (1998) Architecture: Choice or Fate, Windsor, Berkshire, England: Andreas Papadakis. French translation: Architecture: Choix ou Fatalité, Paris: Norma, 1996. Italian translation: Architettura: Scelta o Fatalità, Roma-Bari: Editori Laterza, 1995.
Krier, R. (1979) Urban Space, New York: Rizzoli.
Kunstler, J. H. (1996) Home From Nowhere, New York: Simon & Schuster.
Light, J. (1999) “From City Space to Cyberspace”. In: M. Crang, P. Crang, and J. May (eds.), Virtual Geographies, London: Routledge, 1999, pp. 109-130.
Lotka, A. J. (1926) “The Frequency Distribution of Scientific Productivity”, J. Washington Academy of Sciences, Vol. 16, pp. 317-323.
Lotka, A. J. (1956) Elements of Mathematical Biology, New York: Dover.
Lozano, E. E. (1990) Community Design and the Culture of Cities, Cambridge: Cambridge University Press.
Lynch, K. (1960) The Image of the City, Cambridge, Massachusetts: MIT Press.
Madanipour, A. (1996) Design of Urban Space, Chichester, England: John Wiley.
Makse, H. A., Havlin, S. and Stanley, H. E. (1995) “Modelling Urban Growth Patterns”, Nature, Vol. 377, pp. 608-612.
Mandelbrot, B. B. (1983) The Fractal Geometry of Nature, New York: Freeman.
Mehaffy, M. W. and Salingaros, N. A. (2002) “The End of the Modern World”, PLANetizen, January. < http://www.planetizen.com/node/38>. Reprinted by Open Democracy, February 2002.
Meier, R. L. (1962) A Communications Theory of Urban Growth, Cambridge, Massachusetts: MIT Press.
Mesarovic, M. D., Macko, D. and Takahara, Y. (1970) Theory of Hierarchical Multilevel Systems, New York: Academic Press.
Mikiten, T. M., Salingaros, N. A. and Yu, H. (2000) “Pavements as Embodiments of Meaning for a Fractal Mind”, Nexus Network Journal, Vol. 2, pp. 63-74. Capítulo 7 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Miller, G. A. (1956) “The Magical Number Seven Plus or Minus Two: Some Limits on Our Capacity for Processing Information”, The Psychological Review, Vol. 63, pp. 81-97.
Miller, J. G. (1978) Living Systems, New York: McGraw-Hill.
Moughtin, C. (1992) Urban Design: Street and Square, Oxford: Butterworth.
Moughtin, C, Oc, T. and Tiesdell, S. (1995) Urban Design: Ornament and Decoration, Oxford, England: Butterworth.
Newman, P. and Kenworthy, J. (1999) Sustainability and Cities, Washington D.C.: Island Press.
Nyikos, L., Balazs, L. and Schiller, R. (1994) “Fractal Analysis of Artistic Images: From Cubism to Fractalism”, Fractals, Vol. 2, pp. 143-152.
Pareto, V. (1897) Cours d’Economie Politique, Lausanne, Switzerland.
Parnas, D. L., Clements, P. C. and Weiss, D. M. (1985) “The Modular Structure of Complex Systems”, IEEE Transactions on Software Engineering, SE-11, pp. 259-266.
Passioura, J. B. (1979) “Accountability, Philosophy, and Plant Physiology”, Search (Australian Journal of Science), Vol. 10 No. 10, pp. 347-350.
Paumier, C. B. (1988) Designing the Successful Downtown, Washington, DC: Urban Land Institute.
Peters, R. H. (1983) The Ecological Implications of Body Size, Cambridge: Cambridge University Press.
Portugali, J. (2000) Self- organization and Cities, Heidelberg: Springer-Verlag.
Pree, W. (1995) Design Patterns for Object-Oriented Software Development, Reading, Massachusetts: Addison-Wesley.
Ribeiro, G. (1997) “An Ecological Approach to the Study of Urban Spaces: the Case of a Shantytown in Brasilia”, Journal of Architectural and Planning Research, Vol. 14, pp. 289-300.
Robertson, L. (1995) “A New Theory for Urban Design”, Urban Design Quarterly, Vol. 56, pp. 11-13.
Sahal, D. (1981) Patterns of Technological Innovation, Reading, Massachusetts: Addison-Wesley.
Salingaros, N. A. (1995) “The Laws of Architecture from a Physicist’s Perspective”, Physics Essays , Vol. 8, pp. 638-643. Capítulo 1 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006). Traducción en español: “Las Leyes de la Arquitectura desde la Perspectiva de un Físico”, El Hombre y la Máquina, No 16 (Abril de 2001) páginas 12-23. Republicado en: La Simetria (Febrero de 2002).
Salingaros, N. A. (1997) “Life and Complexity in Architecture From a Thermodynamic Analogy”, Physics Essays, Vol. 10, pp. 165-173. Capítulo 5 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (1998) “A Scientific Basis for Creating Architectural Forms”, Journal of Architectural and Planning Research, Vol. 15, pp. 283-293. Capítulo 2 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (1999) “Architecture, Patterns, and Mathematics”, Nexus Network Journal, Vol 1, pp. 75-85. Capítulo 6 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (2000) “Hierarchical Cooperation in Architecture, and the Mathematical Necessity for Ornament”, Journal of Architectural and Planning Research, Vol. 17, pp. 221-235. Capítulo 3 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Salingaros, N. A. (2001) “Fractals in the New Architecture”, Archimagazine. Reprinted in Katarxis No. 3 (September 2004). Traduzione in italiano: “I Frattali Nella Nuova Architettura”, Archimagazine (2001).
Salingaros, N. A. (2004) “Charles Jencks and the New Paradigm in Architecture”, Part 2 of Anti-Architecture and Deconstruction, Umbau-Verlag, Solingen, 2004, pp. 41-55. Shortened version in Chaos & Complexity Letters, Vol. 1, No. 2 (2004), pp. 101-106. Capítulo 3 de: Anti-Architecture and Deconstruction, Solingen, Germany: Umbau-Verlag (2007).
Salingaros, N. A. and Mikiten, T. M. (2002) “Darwinian Processes and Memes in Architecture: A Memetic Theory of Modernism”, Journal of Memetics—Evolutionary Models of Information Transmission, Vol. 6. Reprinted in: DATUTOP Journal of Architectural Theory, Vol. 23 (2002), pp. 117-139. Capítulo 10 de: A Theory of Architecture, Solingen, Germany: Umbau-Verlag (2006).
Shannon, C. E. and Weaver, W. (1949) The Mathematical Theory of Communication, Urbana: University of Illinois Press.
Simon, H. A. and Ando, A. (1961) “Aggregation of Variables in Dynamic Systems”, Econometrica, Vol. 29, pp. 111-138.
Simon, H. A. (1962) “The Architecture of Complexity”, Proceedings of the American Philosophical Society, Vol. 106, pp. 467-482. Reprinted in: Herbert A. Simon, The Sciences of the Artificial, Cambridge, Massachusetts: MIT Press, 1969, pp. 84-118.
Sörgel, H. (1918) Einführung in die Architektur-Ästhetik, Munich: Piloty & Loehle.
Steen, L. A. (1988) “The Science of Patterns”, Science, Vol. 240, pp. 611-616.
Stringer, P. (1975) “The Myths of Architectural Creativity”, Architectural Design, Vol. 45, pp. 634-635.
Van der Ryn, S. and Cowan, S. (1996) Ecological Design, Washington, D.C.: Island Press.
Ward, V. and Holtham, C. (2000) “The Role of Private and Public Spaces in Knowledge Management”. In: Knowledge Management: Concepts and Controversies, 10-11 February 2000, University of Warwick, Coventry, UK.
Watts, D. J. and Strogatz, S. H. (1998) “Collective Dynamics of ‘Small-World’ Networks”, Nature, Vol. 393, pp. 440-442.
Weaver, W. (1948) “Science and Complexity”, American Scientist, Vol. 36, pp. 536-544.
West, B. J. and Deering, W. (1994) “Fractal Physiology for Physicists: Lévy Statistics”, Physics Reports, Vol. 246, Nos. 1&2, pp. 1-100.
West, B. J. and Deering, B. (1995) The Lure of Modern Science, Singapore: World Scientific.
West, B. J. and Salk, J. (1987) “Complexity, Organization and Uncertainty”, European J. Operations Research, Vol. 30, pp. 117-128.
West, B. J. and Shlesinger, M. (1990) “The Noise in Natural Phenomena”, American Scientist, Vol. 78, pp. 40-45.
Whyte, W. H. (1980) The Social Life of Small Urban Spaces, Washington, D.C.: The Conservation Foundation.
Wiedenhoeft, R. (1981) Cities for People, New York: Van Nostrand Reinhold.
Willis, J. C., (1922) Age and Area: A Study in Geographical Distribution and Origin of Species, Cambridge, England: Cambridge University Press.
Zipf, G. K. (1949) Human Behavior and the Principle of Least Effort, Cambridge, Massachusetts: Addison-Wesley.






