Ocurre muchas veces que un concepto o una idea coge fuerza, se agranda, se encuentra y se resigue en textos, conferencias y libros, y llega con mayor o menor fortuna a recalar en el inconsciente colectivo.
Cuando esto ocurre, pensamos desde una cierta insolencia que estamos descubriendo factores clave que explican nuestra sociedad. Sin que eso deje de ser cierto, es conveniente de vez en cuanto hacer una alto reflexivo en el camino.
Nada surge por generación espontánea. Nada es nuevo, original. Las epifanías ni son ciertas, ni son necesarias. Otra cosa muy diferente es el placer por un descubrimiento personal de algo o alguien que nos ofrece un privilegiado espejo donde mirarnos. La imagen que nos devuelve la leemos como nueva y fascinante para nosotros, pero ¿lo es realmente?
Si hacemos ese pequeño alto en el camino que evocaba antes, y nos ponemos a investigar un poco, veremos que siempre hubo alguien que nos precedió. Aquellas idea que pensábamos rompedoras tiene raíces, habitualmente profundas, que se inmiscuyen en el vector de la historia.
Queda claro que eso no aniquila el pensamiento disruptivo ni que el afán por la novedad sea pernicioso. Queremos avanzar, aprender, mejorar. Eso es consustancial al ser humano, y no solamente no debemos acotarlo, sino todo lo contrario, alentarlo, financiarlo, legitimarlo intelectualmente, socialmente e incluso políticamente.
Investigar, algo que desde la modestia más absoluta y la precariedad de los medios, se intenta hacer aquí, permite descubrir atónito que aquella idea, aquel concepto que pensábamos demoledor, radicalmente nuevo y genuinamente contemporáneo, hace años, lustros y a veces siglos que lo trato con extraordinaria lucidez algún portentoso cerebro. Lejos de desanimar, eso debería legitimar todavía más nuestra concepción y aprender del pasado.
Viene a cuento esta reflexión cuando descubrí, mientras leía el famoso libro de Jane Jacobs The Death and Life of Great American Cities1 de 1961, en el Annual Report of the Rockefeller Foundation de 1958 un escrito Sciences and Complexity de Warren Weaver2 de 1948 donde se hace una explicación diáfana y lúcida del concepto de la complejidad. Parece increíble que aquello a veces pensamos como absolutamente paradigmático de la contemporaneidad, Jacobs ya lo estaba desarrollando en 1961, y el Weaver lo introdujo en 1948 a partir de un texto de 1947.
Pensar lo complejo, en lo complejo, desde lo complejo
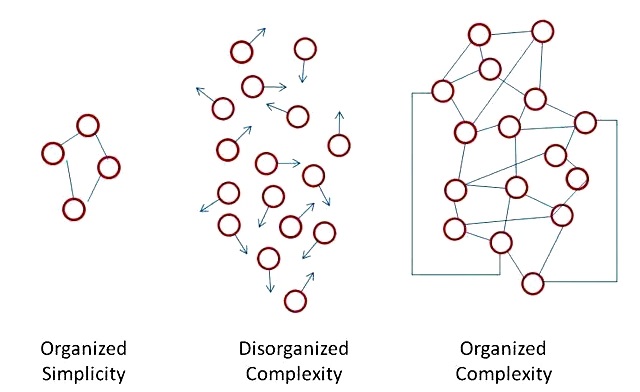
Weaver lista tres estados en el desarrollo de la historia del pensamiento científico:
- Primero: La habilidad para tratar con problemas simples.
- Segundo: La habilidad para tratar con problemas basados en una complejidad desorganizada.
- Tercero: La habilidad para tratar con problemas basados en una complejidad organizada.
Problemas simples
El primer estado, los problemas simples, generan cuestiones que contienen dos factores que están relacionados directamente uno con el otro en su comportamiento, dos variables. Este tipo de problemas de la simplicidad fueron según Weaver el primer tipo de problemas que la ciencia aprendió a atacar.
Usando las palabras del propio Weaver:
Hablando crudamente, uno podría decir que los siglos XVII, XVIII y XIX, formaron el periodo en que las ciencias de la física aprendieron como analizar problemas de dos variables. Durante estos 300 años, la ciencia desarrolló las técnicas experimentales y analíticas para tratar problemas en los que una cantidad, por ejemplo la presión de un gas, depende principalmente de una segunda cantidad, por ejemplo el volumen que ocupa ese mismo gas. El carácter esencial de este problema reside en el hecho de que el comportamiento de la primera cantidad puede ser descrita con un nivel de precisión suficientemente útil, tomando solamente su dependencia con la segunda cantidad y descuidando la menor influencia de otros factores.
Este problema de dos variables es esencialmente simple en su estructura y esa simplicidad fue una condición necesaria para el progreso del estado de desarrollo de la ciencia.
Es más, el vastísimo progreso de pudieron desarrollar las ciencias de la física tanto en teorías como en experimentos, fue gracias a su carácter esencialmente simple.3
Complejidad no organizada
No fue hasta después de 1900 que el segundo método para analizar problemas fue desarrollado por las ciencias de la física. Siguiendo con la argumentación del Weaver:
Algunas mentes imaginativas, además de estudiar ya algunos problemas que manejaban tres o cuatro variables, fueron al otro extremo y pensaron en desarrollar métodos analíticos que pudieran manejar dos billones de variables. Esto es, las ciencias de la física, con las matemáticas habitualmente a la vanguardia, desarrollaron poderosas técnicas en la teoría de la probabilidad y la mecánica estadística que permitieron manejar lo que podríamos llamar complejidad desorganizada.
Consideremos primero una imagen muy simple para coger el perfume de la idea. La dinámica clásica del siglo XIX estaba convenientemente preparada para analizar y predecir el movimiento de una única bola de marfil a lo largo de una mesa de billar. Uno podía, con un sorprendente incremento en la dificultad, analizar el movimiento de dos bolas de billar. Pero cuando se intentaba analizar el movimiento de 10 ó 15 bolas de billar a la vez, el problema se hacía inmanejable, no tanto por culpa de una dificultad teórica, sino porque el trabajo para manejar detalladamente el problema, con tal cantidad de variables era impracticable.
Imaginemos ahora una enorme mesa de billar con millones de bolas corriendo por su superficie. La sorpresa es que ahora el problema se vuelve más simple: los métodos de la mecánica estadística son ahora aplicables. Uno no puede trazar detalladamente la historia de una bola específica, pero se pueden responder con mucha precisión cuestiones tan importantes como: ¿en porcentaje, cuántas bolas por segundo chocarán con una extensión determinada de un lado de la mesa? ¿En porcentaje, cuán lejos se mueve una bola después de chocar con otra?
La palabra desorganizada, de complejidad desorganizada, está aplicada aquí a la enorme mesa, con sus numerosas bolas dispuestas de cualquier manera, pero ignorando el comportamiento de cada una de las bolas individualmente, el sistema como un todo posee un cierto orden y puede analizar porcentajes de las propiedades de éste.
Toda la estructura de la física moderna descansa en estos conceptos estadísticos. En el fondo, toda la cuestión de la evidencia, y la manera en la que el conocimiento interfiere con esta idea de evidencia, está actualmente comprobado que depende de los conceptos antes mencionados. Podríamos llegar a decir que las nociones de probabilidad son esenciales a cualquier teoría del conocimiento.4
Aún así, observa Jacobs, no todos los problemas pueden resolverse con estos métodos analíticos. Las ciencias de la vida, como por ejemplo la biología y la medicina, no pueden ser resueltas así. Estas ciencias han hecho grandes cambios pero se mantienen todavía en lo que el Weaver denomina estados preliminares para la aplicación de análisis, se entiende por supuesto que estamos hablando de 1961. Estas ciencias todavía están centradas en coleccionar, describir, clasificar y observar lo que son aparentemente efectos relacionados.
Complejidad organizada
En este periodo de estado preliminar, aparte de todas las utilísimas cosas que se han aprendido, está también el hecho de que las ciencias de la vida no son problemas simples, ni son problemas de complejidad desorganizada. En si mismo estas ciencias se colocan en un tipo de problemas diferentes, unos problemas cuyos métodos de ataque todavía están bastante atrasados tal como el Weaver describía:
Uno está tentado a sobre-simplificar y decir que la metodología científica fue de un extremo a otro y dejó sin tratar la gran región central entre los dos extremos. La importancia de esta región central de la metodología científica, no depende principalmente del hecho de que el número de variables sea moderado, enorme si lo comparamos con 2 variables y pequeño si lo comparamos con el número de átomos que hay en una pizca de sal. Mucho más importante que el número de variables es el hecho que estas variables están relacionadas. Este tipo de problemas, en contraste con las situaciones de complejidad desorganizada que la estadística puede abarcar, muestran la característica esencial de la organización. Vamos a llamar a este grupo de problemas como problemas de complejidad organizada.
¿Qué es lo que hace que una rosa se abra? ¿Por qué el agua salada no satisface la sed? ¿Qué es un gen, y como la constitución genética original de un organismo vivo llega a expresarse en el desarrollo característico de un adulto?
Ciertamente, todos estos problemas son complejos, pero no son problemas de una complejidad desorganizada, que los métodos estadísticos puedan desentrañar. Son problemas que involucran simultáneamente un número abordable de factores que están interrelacionados en un todo orgánico.5
Es muy interesante, visto desde la actualidad, la acotación a la complejidad organizada que hace el Weaver y que sagazmente apunta Jacobs en la que entre otros se apunta el tema del desarrollo genético. Se va formando así, aunque de manera embrionaria, una línea teórica que en un mismo conjunto de ideas relaciona complejidad con geometría, biología con arquitectura, crecimiento y parámetros geométricos, procesos de desarrollo genético con algoritmos para el desarrollo de nuevas formas arquitectónicas y urbanas etc. En definitiva se empieza a vislumbrar un recorrido a través de un cuerpo de conocimiento. En un resumen extremo este cuerpo del conocimiento relaciona en términos muy generales la arquitectura con la idea de lo orgánico.
El propio Weaver especulaba en 1948, en el umbral del hiperdesarrollo de las ciencias de la vida, que si éstas hacían un significativo progreso en resolver este tipo de problemas
entonces habrán oportunidades para extender estas nuevas técnicas, aunque sea solamente por analogía, a vastas áreas de las ciencias del comportamiento y las ciencias sociales.[6]
En los 25 años posteriores a esa afirmación, las ciencias de la vida experimentaron de hecho un inmenso y brillante progreso. Efectivamente, estas ciencias han acumulado con ímpetu extraordinario una gran cantidad de conocimiento. Igualmente mejoraron tanto el cuerpo teórico como los procedimientos de forma que abrieron un gran número de cuestiones nuevas, mostrando solamente que ese progreso sólo había sido el principio de una enorme esfera del conocimiento donde acceder.
Este progreso sólo fue posible, según Jacobs, ya que las ciencias de la vida reconocieron los problemas en el ámbito de la complejidad organizada, de manera que pudieron ser pensadas y atacadas entendiendo el tipo de problema que representaban. Este progreso también nos deja una lección tremendamente importante acerca de los problemas basados en una complejidad organizada. Nos dice que este tipo de problemas permiten ser analizados, que es la única manera de ser comprendidos, en vez de ser considerados tal y como decía el Weaver como
algo que ponemos en la oscuridad de lo irracional.
Una vez establecidos los principios básicos del concepto de la complejidad organizada, Jacobs nos invita a explorar qué es lo que este tipo de razonamiento puede hacer por la ciudad.
Han pasado unos cuantos años desde entonces, y todavía estamos en ello.
Miquel Lacasta Codorniu. Doctor arquitecto
Barcelona, Mayo 2015
Notas:
1 Jacobs, Jane, The Death and Life of Great American Cities, Modern Library Edition, Random House, 1993, (1961), Nueva York
2 Weaver, Warren, “A Quarter Century in Natural Science”, Cap. 1 “Science and Complexity”, Annual Report of the Rockefeller Foundation, Nueva York, 1958, pp. 1-123 Una versión se puede encontrar en http://philoscience.unibe.ch/documents/uk/weaver1948.pdf
3 Op. Cit., Jacobs p. 560.
4 Ibídem, p. 562
5 Ibídem, p.563.
6 Ibídem, p. 564.






